
【题目】阅读如图所示的程序框图,则该算法的功能是( ) 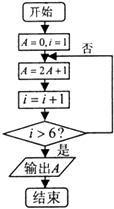
A.计算数列{2n﹣1}前5项的和
B.计算数列{2n﹣1}前5项的和
C.计算数列{2n﹣1}前6项的和
D.计算数列{2n﹣1}前6项的和
【答案】C
【解析】解:由算法的流程知,第一次运行,A=2×0+1=1,i=1+1=2;
第二次运行,A=2×1+1=3,i=2+1=3;
第三次运行,A=2×3+1=7,i=3+1=4;
第四次运行,A=2×7+1=15,i=5;
第五次运行,A=2×15+1=31,i=6;
第六次运行,A=2×31+1=63,i=7;满足条件i>6,终止运行,输出A=63,
∴A=1+2+22+…+25= ![]() =26﹣1=64﹣1=63.
=26﹣1=64﹣1=63.
故选:C.
【考点精析】本题主要考查了程序框图的相关知识点,需要掌握程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设函数y=f(x)由方程x|x|+y|y|=1确定,下列结论正确的是(请将你认为正确的序号都填上)
·(1)f(x)是R上的单调递减函数;
·(2)对于任意x∈R,f(x)+x>0恒成立;
·(3)对于任意a∈R,关于x的方程f(x)=a都有解;
·(4)f(x)存在反函数f﹣1(x),且对于任意x∈R,总有f(x)=f﹣1(x)成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若样本![]() 的平均数是
的平均数是![]() ,方差是
,方差是![]() ,则对样本
,则对样本![]() ,下列结论正确的是 ( )
,下列结论正确的是 ( )
A. 平均数为14,方差为5 B. 平均数为13,方差为25
C. 平均数为13,方差为5 D. 平均数为14,方差为2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在钝角△ABC中,∠A为钝角,令 ![]() =
= ![]() ,
, ![]() =
= ![]() ,若
,若 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R).现给出下面结论:
(x,y∈R).现给出下面结论:
①当x= ![]() 时,点D是△ABC的重心;
时,点D是△ABC的重心;
②记△ABD,△ACD的面积分别为S△ABD , S△ACD , 当x= ![]() 时,
时, ![]() ;
;
③若点D在△ABC内部(不含边界),则 ![]() 的取值范围是
的取值范围是 ![]() ;
;
④若 ![]() =λ
=λ ![]() ,其中点E在直线BC上,则当x=4,y=3时,λ=5.
,其中点E在直线BC上,则当x=4,y=3时,λ=5.
其中正确的有(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:

(1)求分数在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有5个大小相同的球,其中有2个白球,2个黑球,1个红球,现从袋中每次取出1球,去除后不放回,直到取到有两种不同颜色的球时即终止,用![]() 表示终止取球时所需的取球次数,则随机变量
表示终止取球时所需的取球次数,则随机变量![]() 的数字期望
的数字期望![]() 是( )
是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x+λ3﹣x(λ∈R).
(1)若f(x)为奇函数,求λ的值和此时不等式f(x)>1的解集;
(2)若不等式f(x)≤6对x∈[0,2]恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=![]() , AB=2,CD=3,M为PC上一点,PM=2MC.
, AB=2,CD=3,M为PC上一点,PM=2MC.
(Ⅰ)证明:BM∥平面PAD;
(Ⅱ)若AD=2,PD=3,求二面角D﹣MB﹣C的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com