Question

9．已知抛物线y²=4x的准线与x轴交于点P，过点P且斜率为k（k＞0）的直线l与抛物线交于A，B两点，F为抛物线的焦点，若|FB|=2|FA|，则k的值为（　　）

• A． $\frac{1}{3}$
• B． $\frac{{\sqrt{2}}}{3}$
• C． $\frac{2}{3}$
• D． $\frac{{2\sqrt{2}}}{3}$

Answer 1

分析 设出A，B的坐标，再设出AB的方程，联立直线方程和抛物线方程，由焦半径结合|FA|=3|FB|，求得A的坐标，代入两点求斜率公式得答案．

解答 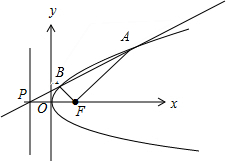解：设A（x₁，y₁），B（x₂，y₂），
由已知2|FA|=|FB|，得：x₂+1=2（x₁+1），即x₂=2x₁+1，①
∵P（-1，0），则AB的方程：y=kx+k，
与y²=4x联立，得：k²x²+（2k²-4）x+k²=0，则x₁x₂=1，②
由①②得x₁=$\frac{1}{2}$，则A（2，2$\sqrt{2}$），
∴k=$\frac{2\sqrt{2}-0}{2+1}$=$\frac{2\sqrt{2}}{3}$，
故选：D．

点评 本题主要考查了抛物线的简单性质．考查了直线与抛物线的关系及焦点弦的问题．常需要利用抛物线的定义来解决．