Question

7．在平面直角坐标系xOy中，已知点A是半圆x²-4x+y²=0（2≤x≤4）上的一个动点，点C在线段OA的延长线上，当$\overrightarrow{OA}•\overrightarrow{OC}$=20时，点C的轨迹为（　　）

• A． 椭圆一部分
• B． 抛物线一段
• C． 线段
• D． 圆弧

Answer 1

分析 设出C点坐标，把A的坐标用α表示，得到|OA|，结合$\overrightarrow{OA}•\overrightarrow{OC}=20$中结论求出C的横坐标为定值5，进一步求出C的纵坐标的范围，则点C的轨迹可求．

解答 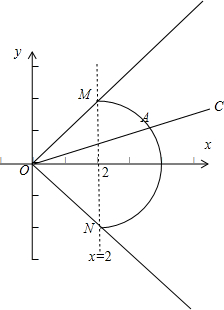解：设C（x，y），A（2+2cosα，sinα），其中-$\frac{π}{2}$≤α≤$\frac{π}{2}$，
则∠xOC=$\frac{α}{2}$．
∵|OA|²=（2+2cosα）²+（2sinα）²=8（1+cosα）=16$co{s}^{2}\frac{α}{2}$，
∴|OA|=4cos$\frac{α}{2}$．
由$\overrightarrow{OA}•\overrightarrow{OC}=20$得：|OC|cos$\frac{α}{2}$=5，∴x=|OC|cos$\frac{α}{2}$=5．
从而y=|OC|sin$\frac{α}{2}$=5tan$\frac{α}{2}$∈[-5，5]．
故点C的轨迹是一条线段，其两个短点的坐标分别为A（5，5），B（5，-5）．
故选：C．

点评 本题考查了轨迹方程，考查了数形结合的解题思想方法和数学转化思想方法，解答的关键是利用平面几何知识把未知长度的式子转化为已知长度的式子，是中档题．