练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知在平面直角坐标系中，圆的参数方程为（为参数）．以原点为极点，轴的非负半轴为极轴，取相同的单位长度建立极坐标系．

    （1）求圆的普通方程及其极坐标方程；

    （2）设直线的极坐标方程为，射线与圆的交点为（异于极点），与直线的交点为，求线段的长．

    【答案】(1) 普通方程为： ; 极坐标方程为：．(2)

    【解析】

    （1）由圆的参数方程消去参数，得到普通方程，再由直角坐标与极坐标的互化公式，得到极坐标方程；

    （2）将代入圆的极坐标方程，得到；将代入直线的极坐标方程，得到，再由，即可得出结果.

    （1）由

    平方相加，得：，

    所以圆的普通方程为：

    又，，∴

    化简得圆的极坐标方程为：．

    （2）把代入圆的极坐标方程可得：

    把代入直线的极坐标方程可得：， ∴

    所以线段的长

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数在内有两个零点，则实数的取值范围是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）若函数f（x）在（0，+∞）上是减函数，其实数m的取值范围；

    （2）若函数f（x）在（0，+∞）上存在两个极值点x1，x2，证明：lnx1+lnx2＞2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）判断函数在区间上零点的个数；

    （2）函数在区间上的极值点从小到大分别为，证明：

    （Ⅰ）；

    （Ⅱ）对一切成立.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，是等边三角形， 是边上的动点（含端点），记,.

    （1）求的最大值；

    （2）若，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝ex﹣lnx+ax（a∈R）．

    （1）当a＝﹣e+1时，求函数f（x）的单调区间；

    （2）当a≥﹣1时，求证：f（x）＞0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】的内角，，所对边分别为，，.已知.

    (1) 求；

    (2) 若为锐角三角形，且，求面积的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （1）讨论函数的单调性；

    （2）当时， 恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

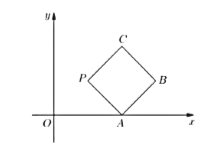
    【题目】如图所示，在平面直角坐标系上放置一个边长为1的正方形，此正方形沿轴滚动（向左或者向右均可），滚动开始时，点在原点处，例如：向右滚动时，点的轨迹起初时以点为圆心，1为半径的圆弧，然后以点与轴交点为圆心，长度为半径……，设点的纵坐标与横坐标的函数关系式是，该函数相邻两个零点之间的距离为.

    （1）写出的值，并求出当时，点轨迹与轴所围成的图形的面积，研究该函数的性质并填写下面的表格：

    函数性质

    结论

    奇偶性

    单调性

    递增区间

    递减区间

    零点

    （2）已知方程在区间上有11个根，求实数的取值范围

    （3）写出函数的表达式.

    查看答案和解析>>

    同步练习册答案