
【题目】已知函数![]() .
.
(1)若函数f(x)在(0,+∞)上是减函数,其实数m的取值范围;
(2)若函数f(x)在(0,+∞)上存在两个极值点x1,x2,证明:lnx1+lnx2>2.
【答案】(1)![]() .(2)证明见解析
.(2)证明见解析
【解析】
(1)由题知![]() 在
在![]() 上恒成立.参变分离求实数m的取值范围即可.
上恒成立.参变分离求实数m的取值范围即可.
(2)求导代入极值点分析![]() 满足的关系式,再代换
满足的关系式,再代换![]() 构造出关于
构造出关于![]() 的方程,再换元证明不等式即可.
的方程,再换元证明不等式即可.
(1)由函数f(x)在(0,+∞)上是减函数,可知,f′(x)=lnx﹣mx≤0恒成立,
∴m![]() 恒成立,故m
恒成立,故m![]() max,
max,
令g(x)![]() ,x>0,
,x>0,
则g′(x)![]() ,
,
当x∈(0,e),g′(x)![]() 0,g(x)单调递增,
0,g(x)单调递增,
当x∈(e,+∞),则g′(x)![]() 0,g(x)单调递减,
0,g(x)单调递减,
g(x)max=g(e)![]() ,
,
∴![]() .
.
(2)由(1)f′(x)=lnx﹣mx,
由f(x)在(0,+∞)上存在两个极值点,不妨设x1<x2,
知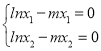 ,
,
则m![]() ,
,
又m![]() ,
,
∴![]() ,
,
即lnx1+lnx2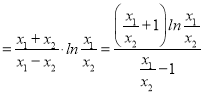 ,
,
设t![]() ∈(0,1),
∈(0,1),
要证明:lnx1+lnx2>2,
只要证![]() ,
,
只要证lnt![]() ,
,
即证lnt![]() 0,
0,
构造函数h(t)=lnt![]() ,
,
h′(t)![]() 0,
0,
h(t)在(0,1)上单调递增,
∴h(t)<h(1)=0,
即h(t)=lnt![]() 0,
0,
∴lnx1+lnx2>2.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖促销活动,规定每位顾客从装有0、1、2、3的四个相同小球的抽奖箱中,每次取出一球记下编号后放回(连续取两次),若取出的两个小球的编号相加之和等于6,则中一等奖,等于5中二等奖,等于4或3中三等奖,则顾客抽奖中三等奖的概率为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,直线l过点
,直线l过点![]() 且与x轴不重合,l交圆
且与x轴不重合,l交圆![]() 于C,D两点,过
于C,D两点,过![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点E.设点E的轨迹为
于点E.设点E的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 相切于点M,
相切于点M,![]() 与两坐标轴的交点为A与B,直线
与两坐标轴的交点为A与B,直线![]() 经过点M且与
经过点M且与![]() 垂直,
垂直,![]() 与
与![]() 的另一个交点为N,当
的另一个交点为N,当![]() 取得最小值时,求
取得最小值时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第28届金鸡百花电影节将于11月19日至23日在福建省厦门市举办,近日首批影展片单揭晓,《南方车站的聚会》《春江水暖》《第一次的离别》《春潮》《抵达之谜》五部优秀作品将在电影节进行展映.若从这五部作品中随机选择两部放在展映的前两位,则《春潮》与《抵达之谜》至少有一部被选中的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N*,存在实数x使f(x)<2成立.
(1)求实数m的值;
(2)若α≥1,β≥1,f(α)+f(β)=4,求证:![]() ≥3.
≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]() .某医疗设备公司生产某医疗器材,已知每月生产
.某医疗设备公司生产某医疗器材,已知每月生产![]() 台
台![]() 的收益函数为
的收益函数为![]() (单位:万元),成本函数
(单位:万元),成本函数![]() (单位:万元),该公司每月最多生产
(单位:万元),该公司每月最多生产![]() 台该医疗器材.(利润函数=收益函数-成本函数)
台该医疗器材.(利润函数=收益函数-成本函数)
(1)求利润函数![]() 及边际利润函数
及边际利润函数![]() ;
;
(2)此公司每月生产多少台该医疗器材时每台的平均利润最大,最大值为多少?(精确到![]() )
)
(3)求![]() 为何值时利润函数
为何值时利润函数![]() 取得最大值,并解释边际利润函数
取得最大值,并解释边际利润函数![]() 的实际意义.
的实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的单位长度建立极坐标系.
轴的非负半轴为极轴,取相同的单位长度建立极坐标系.
(1)求圆![]() 的普通方程及其极坐标方程;
的普通方程及其极坐标方程;
(2)设直线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() (异于极点),与直线
(异于极点),与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,在线段
,在线段![]() 上任取两点(端点A,B除外 ),将线段
上任取两点(端点A,B除外 ),将线段![]() 分成了三条线段,若分成的三条线段长度均为正整数,则这三条线段可以构成三角形的概率是 ____________;若分成的三条线段的长度均为正实数,则这三条线段可以构成三角形的概率是 _________.
分成了三条线段,若分成的三条线段长度均为正整数,则这三条线段可以构成三角形的概率是 ____________;若分成的三条线段的长度均为正实数,则这三条线段可以构成三角形的概率是 _________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com