
【题目】已知圆![]() 的圆心为
的圆心为![]() ,直线l过点
,直线l过点![]() 且与x轴不重合,l交圆
且与x轴不重合,l交圆![]() 于C,D两点,过
于C,D两点,过![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点E.设点E的轨迹为
于点E.设点E的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 相切于点M,
相切于点M,![]() 与两坐标轴的交点为A与B,直线
与两坐标轴的交点为A与B,直线![]() 经过点M且与
经过点M且与![]() 垂直,
垂直,![]() 与
与![]() 的另一个交点为N,当
的另一个交点为N,当![]() 取得最小值时,求
取得最小值时,求![]() 的面积.
的面积.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)根据三角形相似得到![]() ,得到AE+DE=4,再利用椭圆定义求解即可
,得到AE+DE=4,再利用椭圆定义求解即可
(2)设![]() 的方程为
的方程为![]() ,与椭圆联立,由直线
,与椭圆联立,由直线![]() 与
与![]() 相切得
相切得![]() ,由
,由![]() 在x轴、y轴上的截距分别为
在x轴、y轴上的截距分别为![]() ,m,得
,m,得![]() 表达式,结合基本不等式求得
表达式,结合基本不等式求得![]() 坐标及
坐标及![]() ,进而得
,进而得![]() ,则面积可求
,则面积可求
(1)因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,则
,则![]() ,
,
所以![]() ,从而
,从而![]() .
.
![]() 化为
化为![]() ,
,
所以![]() ,
,
从而E的轨迹为以![]() ,
,![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆(剔除左、右顶点).
的椭圆(剔除左、右顶点).
所以![]() 的方程为
的方程为![]() .
.
(2)易知![]() 的斜率存在,所以可设
的斜率存在,所以可设![]() 的方程为
的方程为![]() ,
,
联立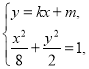 消去y,得
消去y,得![]() .
.
因为直线l与![]() 相切,所以
相切,所以![]() ,
,
即![]() .
.
![]() 在x轴、y轴上的截距分别为
在x轴、y轴上的截距分别为![]() ,m,
,m,
则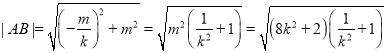
![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
所以当![]() 时,
时,![]() 取得最小值,此时
取得最小值,此时![]() ,
,
根据对称性.不妨取![]() ,
,![]() ,此时
,此时![]() ,
,
即![]() ,从而
,从而![]() .
.
联立 消去y,得
消去y,得![]() ,
,
则![]() ,解得
,解得![]() ,
,
所以![]() ,故
,故![]() 的面积为
的面积为![]() .
.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() :
:![]() 上的一动点,点
上的一动点,点![]() ,点
,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设曲线![]() 与
与![]() 轴的正半轴,
轴的正半轴,![]() 轴的正半轴的交点分别为点
轴的正半轴的交点分别为点![]() ,
,![]() ,斜率为
,斜率为![]() 的动直线
的动直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,其中点
两点,其中点![]() 在第一象限,求四边形
在第一象限,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道![]() 和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是
列联表,已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.4.
地区当中“非常满意”的观众的概率为0.4.
非常满意 | 满意 | 合计 | |
| 35 | 10 |
|
|
|
|
|
合计 |
|
|
|
(1)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“非常满意”的![]() 、
、![]() 地区的人数各是多少.
地区的人数各是多少.
(2)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
附:参考公式:![]() .
.
(3)若以抽样调查的频率为概率,从![]() 、
、![]() 两个地区随机抽取2人,设抽到的观众“非常满意”的人数为
两个地区随机抽取2人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
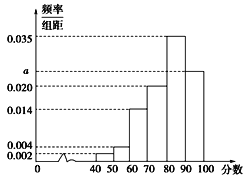
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.

(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数f(x)在(0,+∞)上是减函数,其实数m的取值范围;
(2)若函数f(x)在(0,+∞)上存在两个极值点x1,x2,证明:lnx1+lnx2>2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com