
【题目】由中央电视台综合频道![]() 和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是
列联表,已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.4.
地区当中“非常满意”的观众的概率为0.4.
非常满意 | 满意 | 合计 | |
| 35 | 10 |
|
|
|
|
|
合计 |
|
|
|
(1)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“非常满意”的![]() 、
、![]() 地区的人数各是多少.
地区的人数各是多少.
(2)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
附:参考公式:![]() .
.
(3)若以抽样调查的频率为概率,从![]() 、
、![]() 两个地区随机抽取2人,设抽到的观众“非常满意”的人数为
两个地区随机抽取2人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
【答案】(1) ![]() 地7人、
地7人、![]() 地8人;(2)表格见解析,没有
地8人;(2)表格见解析,没有![]() 的把握认为观众的满意程度与所在地区有关系.(3)分布列见解析,
的把握认为观众的满意程度与所在地区有关系.(3)分布列见解析,![]()
【解析】
(1)“在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.4”,求得
地区当中“非常满意”的观众的概率为0.4”,求得![]() 的值,再根据分层抽样的知识求得应抽取“非常满意”的
的值,再根据分层抽样的知识求得应抽取“非常满意”的![]() 、
、![]() 地区的人数.
地区的人数.
(2)利用公式计算出![]() 的值,由此判断出没有
的值,由此判断出没有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
(3)根据二项分布的分布列计算公式,计算出![]() 的分布列,并求得数学期望.
的分布列,并求得数学期望.
(1)由题意,得:![]() ,解得
,解得![]() ,故
,故![]() .
.
![]() 地抽取
地抽取![]() 人,
人,![]() 地抽取
地抽取![]() 人.
人.
(2)完成表格如下:
非常满意 | 满意 | 合计 | |
| 35 | 10 | 45 |
| 40 | 15 | 55 |
合计 | 75 | 25 | 100 |
![]()
![]() ,
,
![]() 没有
没有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
(3)从![]() 、B两地区随机抽取1人,抽到的观众“非常满意”的概率为
、B两地区随机抽取1人,抽到的观众“非常满意”的概率为![]() ,
,
随机抽取2人,![]() 的可能取值为0,1,2,
的可能取值为0,1,2,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
![]()


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,经过
,经过![]() 轴正半轴上点
轴正半轴上点![]() 的直线
的直线![]() 交
交![]() 于不同的两点
于不同的两点![]() 和
和![]() .
.
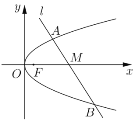
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() ,求证:原点
,求证:原点![]() 总在以线段
总在以线段![]() 为直径的圆的内部;
为直径的圆的内部;
(3)若![]() ,且直线
,且直线![]() ∥
∥![]() ,
,![]() 与
与![]() 有且只有一个公共点
有且只有一个公共点![]() ,问:△
,问:△![]() 的面积是否存在最小值?若存在,求出最小值,并求出
的面积是否存在最小值?若存在,求出最小值,并求出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国的第一艘航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架“歼-15”舰载机准备着舰,已知乙机不能最先着舰,丙机必须在甲机之前着舰(不一定相邻),那么不同的着舰方法种数为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖促销活动,规定每位顾客从装有0、1、2、3的四个相同小球的抽奖箱中,每次取出一球记下编号后放回(连续取两次),若取出的两个小球的编号相加之和等于6,则中一等奖,等于5中二等奖,等于4或3中三等奖,则顾客抽奖中三等奖的概率为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的极值;
的极值;
(2)问:是否存在实数![]() ,使得
,使得![]() 有两个相异零点?若存在,求出
有两个相异零点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道![]() 和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是
列联表,已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“满意”的观众的概率为0.15.
地区当中“满意”的观众的概率为0.15.

(1)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“满意”的![]() 、
、![]() 地区的人数各是多少;
地区的人数各是多少;
(2)在(1)的条件下,从抽取到“满意”的人中随机抽取2人,设“抽到的观众来自不同的地区”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(3)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.

附:参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求曲线![]() 在
在![]() 处的切线的方程;
处的切线的方程;
(2)若对于任意实数![]() ,
,![]() 恒成立,试确定
恒成立,试确定![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,直线l过点
,直线l过点![]() 且与x轴不重合,l交圆
且与x轴不重合,l交圆![]() 于C,D两点,过
于C,D两点,过![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点E.设点E的轨迹为
于点E.设点E的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 相切于点M,
相切于点M,![]() 与两坐标轴的交点为A与B,直线
与两坐标轴的交点为A与B,直线![]() 经过点M且与
经过点M且与![]() 垂直,
垂直,![]() 与
与![]() 的另一个交点为N,当
的另一个交点为N,当![]() 取得最小值时,求
取得最小值时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]() .某医疗设备公司生产某医疗器材,已知每月生产
.某医疗设备公司生产某医疗器材,已知每月生产![]() 台
台![]() 的收益函数为
的收益函数为![]() (单位:万元),成本函数
(单位:万元),成本函数![]() (单位:万元),该公司每月最多生产
(单位:万元),该公司每月最多生产![]() 台该医疗器材.(利润函数=收益函数-成本函数)
台该医疗器材.(利润函数=收益函数-成本函数)
(1)求利润函数![]() 及边际利润函数
及边际利润函数![]() ;
;
(2)此公司每月生产多少台该医疗器材时每台的平均利润最大,最大值为多少?(精确到![]() )
)
(3)求![]() 为何值时利润函数
为何值时利润函数![]() 取得最大值,并解释边际利润函数
取得最大值,并解释边际利润函数![]() 的实际意义.
的实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com