
在曲线C1: (θ为参数,0≤θ<2π)上求一点,使它到直线C2:
(θ为参数,0≤θ<2π)上求一点,使它到直线C2: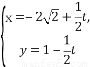 (t为参数)的距离最小,并求出该点坐标和最小距离.
(t为参数)的距离最小,并求出该点坐标和最小距离.
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:填空题
设函数f(x)= D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十第十章第七节练习卷(解析版) 题型:选择题
将一枚硬币连掷5次,如果出现k次正面向上的概率等于出现k+1次正面向上的概率,那么k的值为( )
(A)0 (B)1 (C)2 (D)3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,曲线C1的参数方程为 (φ为参数),曲线C2的参数方程为
(φ为参数),曲线C2的参数方程为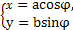 (a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=
(a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=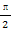 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值.
(2)设当α= 时,l与C1,C2的交点分别为A1,B1,当α=-
时,l与C1,C2的交点分别为A1,B1,当α=- 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十五选修4-2第二节练习卷(解析版) 题型:解答题
已知△ABC,A(-1,0),B(3,0),C(2,1),对它先作关于x轴的反射变换,再将所得图形绕原点逆时针旋转90°.
(1)分别求两次变换所对应的矩阵M1,M2.
(2)求△ABC在两次连续的变换作用下所得到的△A'B'C'的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:选择题
随机变量ξ的分布列如下:
ξ | -1 | 0 | 1 |
P | a | b | c |
其中a,b,c成等差数列,若E(ξ)= ,则D(ξ)的值是( )
,则D(ξ)的值是( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
离散型随机变量X的概率分布规律为P(X=n)=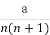 (n=1,2,3,4),其中a是常数,则P(
(n=1,2,3,4),其中a是常数,则P( <X<
<X< )的值为( )
)的值为( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com