
设函数f(x)= D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十八第六章第四节练习卷(解析版) 题型:选择题
某公司一年购买某种货物400吨,每次都购买x吨,运费为4万元/次,一年的总存储费用为4x万元,要使一年的总运费与总存储费用之和最小,则x=( )
(A)20 (B)10 (C)16 (D)8
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:填空题
已知P(x0,y0)是抛物线y2=2px(p>0)上的一点,过P点的切线方程的斜率可通过如下方式求得:
在y2=2px两边同时求导,得:
2yy'=2p,则y'=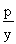 ,所以过P的切线的斜率:k=
,所以过P的切线的斜率:k=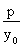 .
.
试用上述方法求出双曲线x2-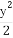 =1在P(
=1在P(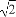 ,
,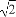 )处的切线方程为 .
)处的切线方程为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:填空题
已知数列{an}中,a1=1,a2=2,当整数n>1时,Sn+1+Sn-1=2(Sn+S1)都成立,则S5= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:选择题
已知数列{an}的通项公式是an=2n-3( )n,则其前20项和为( )
)n,则其前20项和为( )
(A)380- (1-
(1-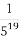 )(B)400-
)(B)400- (1-
(1-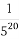 )
)
(C)420- (1-
(1-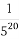 )(D)440-
)(D)440- (1-
(1-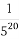 )
)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:选择题
若x,y满足约束条件 且目标函数z=ax+by(a>0,b>0)的最大值为7,则
且目标函数z=ax+by(a>0,b>0)的最大值为7,则 +
+ 的最小值为( )
的最小值为( )
(A)14 (B)7 (C)18 (D)13
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:选择题
若不等式Ax+By+5<0表示的平面区域不包括点(2,4),且k=A+2B,则k的取值范围是( )
(A)k≥- (B)k≤-
(B)k≤-
(C)k>- (D)k<-
(D)k<-
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:选择题
已知Sn是等差数列{an}的前n项和,若a1=-10,a4+a6=-4,则当Sn取最小值时,n=( )
(A)5(B)6(C)11(D)5或6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷(解析版) 题型:解答题
在曲线C1: (θ为参数,0≤θ<2π)上求一点,使它到直线C2:
(θ为参数,0≤θ<2π)上求一点,使它到直线C2: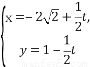 (t为参数)的距离最小,并求出该点坐标和最小距离.
(t为参数)的距离最小,并求出该点坐标和最小距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com