已知函数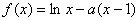
（1）试讨论函数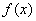
的单调性；
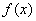（2）若函数在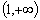
是单调减函数，求实数
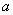的取值范围；
（3）在（2）的条件下，当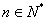
时，证明：
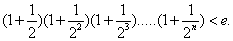（其中（e≈2.718……即自然对数的底数）
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案科目：高中数学 来源： 题型：
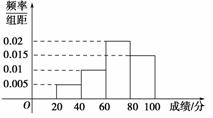
某班
的全体学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为：[20,40)，[40,60)，[60,80)，[80,100]．若低于60分的人数是15，则该班的学生人数是( )
(A)45 (B)50
(C)55 (D)60
查看答案和解析>>
科目：高中数学 来源： 题型：
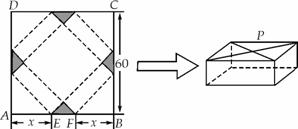
.如图，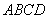
是边长为60 cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，得
、
、
、
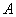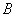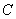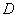四个点重合于图中的点
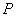，正好形成一个正四棱柱形状的包装盒，
、
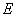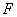在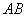
上，是被切去的一个等腰直角三角形斜边的两个端点.设
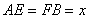cm.若要使包装盒的侧面积最大，则
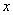的值为______.
查看答案和解析>>
科目：高中数学 来源： 题型：
用反证法证明命题“若整系数的一元二次方程ax2＋bx＋c＝0(a≠0)有有理根，那么a，b，c中至少有一个是偶数”时，下列假设中正确的是 ( )
A．假设a，b，c都是偶数
B．假设a，b，c都不是偶数
C．假设a，b，c至多有一个是偶数
D．假设a，b，c至多有两个偶数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
定义域为
时,
时,
的单调增区间为
无极小值 
函数
...7分
的
张卡片放入
个不同的信封中，若每个信封放
张，其中标号为
的卡片放入同一信封，则有 种不同的放法． （用数字作答）
成立，则实数a的取值范围是 .
，则满足
的
的取值范围是 ( )
，2] B．[0，2] C．
D． 
，
.
和集合
；
，求
在约束条件
下仅在点
处取得最小值，则实数
的取值
范围是 .