
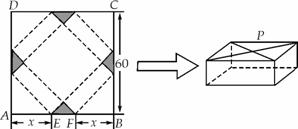
.如图,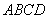 是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得
是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得 、
、 、
、 、
、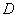 四个点重合于图中的点
四个点重合于图中的点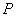 ,正好形成一个正四棱柱形状的包装盒,
,正好形成一个正四棱柱形状的包装盒,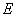 、
、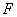 在
在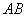 上,是被切去的一个等腰直角三角形斜边的两个端点.设
上,是被切去的一个等腰直角三角形斜边的两个端点.设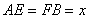 cm.若要使包装盒的侧面积最大,则
cm.若要使包装盒的侧面积最大,则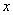 的值为______.
的值为______.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
已知函数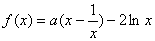 ,
,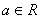 .
.
(1)若a=1,判断函数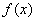 是否存在极值,若存在,求出极值;若不存在,说明理由;
是否存在极值,若存在,求出极值;若不存在,说明理由;
(2)求函数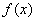 的单调区间;
的单调区间;
(3)设函数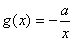 .若至少存在一个
.若至少存在一个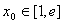 ,使得
,使得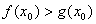 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数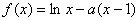
(1)试讨论函数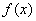 的单调性;
的单调性;
(2)若函数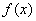 在
在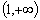 是单调减函数,求实数
是单调减函数,求实数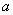 的取值范围;
的取值范围;
(3)在(2)的条件下,当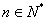 时,证明:
时,证明:
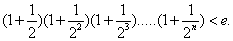 (其中(e≈2.718……即自然对数的底数)
(其中(e≈2.718……即自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
现有某种细胞100个,其中有占约总数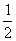 的细胞每小时分裂一次,即由1个细胞分裂成2个细胞,按这种规律发展下去,经过10小时,细胞总数大约为 ( )
的细胞每小时分裂一次,即由1个细胞分裂成2个细胞,按这种规律发展下去,经过10小时,细胞总数大约为 ( )
A.3844个 B.5766个 C.8650个 D.9998个
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=|log2x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m,n的值分别为( )
A.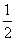 ,2 B.
,2 B.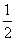 ,4
,4
C.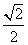 ,
, D.
D.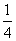 ,4
,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com