
已知函数f(x)=|log2x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m,n的值分别为( )
A.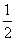 ,2 B.
,2 B.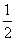 ,4
,4
C.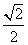 ,
, D.
D.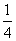 ,4
,4
科目:高中数学 来源: 题型:
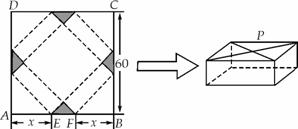
.如图,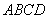 是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得
是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得 、
、 、
、 、
、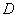 四个点重合于图中的点
四个点重合于图中的点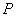 ,正好形成一个正四棱柱形状的包装盒,
,正好形成一个正四棱柱形状的包装盒,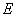 、
、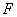 在
在 上,是被切去的一个等腰直角三角形斜边的两个端点.设
上,是被切去的一个等腰直角三角形斜边的两个端点.设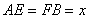 cm.若要使包装盒的侧面积最大,则
cm.若要使包装盒的侧面积最大,则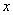 的值为______.
的值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
用反证法证明命题“若整系数的一元二次方程ax2+bx+c=0(a≠0)有有理根,那么a,b,c中至少有一个是偶数”时,下列假设中正确的是 ( )
A.假设a,b,c都是偶数
B.假设a,b,c都不是偶数
C.假设a,b,c至多有一个是偶数
D.假设a,b,c至多有两个偶数
查看答案和解析>>
科目:高中数学 来源: 题型:
为了得到函数y=log2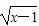 的图象,可将函数y=log2x的图象上所有的点( )
的图象,可将函数y=log2x的图象上所有的点( )
A.纵坐标缩短到原来的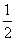 ,横坐标不变,再向右平移1个单位
,横坐标不变,再向右平移1个单位
B.纵坐标缩短到原来的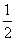 ,横坐标不变,再向左平移1个单位
,横坐标不变,再向左平移1个单位
C.横坐标伸长到原来的2倍,纵坐标不变,再向左平移1个单位
D.横坐标伸长到原来的2倍,纵坐标不变,再向右平移1个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
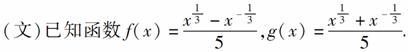
(1)证明f(x)是奇函数,并求其单调区间;
(2)分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,并由此概括一个涉及函数f(x)、g(x)的对所有非零实数x都成立的等式,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
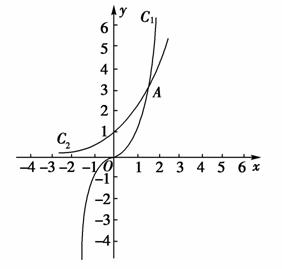
函数f(x)=2x和g(x)=x3的图象的示意图如图所示.设两函数的图象交于点A(x1,y1)、B(x2,y2),且x1<x2.
(1)请指出示意图中曲线C1、C2分别对应哪一个函数?
(2)若x1∈[a,a+1],x2∈[b,b+1],且a、b∈{1,2,3,4,5,6,7,8,9,10,11,12},指出a、b的值,并说明理由;
(3)结合函数图象示意图,请把f(8)、g(8)、f(2012)、g(2012)四个数按从小到大的顺序排列.
查看答案和解析>>
科目:高中数学 来源: 题型:
某加工厂需定期购买原材料,已知每公斤原材料的价格为1.5元,每次购买原材料需支付运费600元.每公斤原材料每天的保管费用为0.03元,该厂每天需消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管).
(1)设该厂每x天购买一次原材料,试写出每次购买的原材料在x天内总的保管费用y1(元)关于x的函数关系式;
(2)求该厂多少天购买一次原材料才能使平均每天支付的总费用y(元)最少,并求出这个最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com