
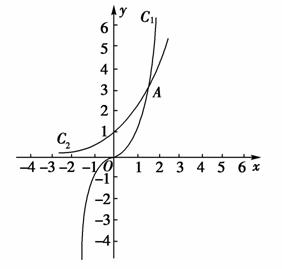
函数f(x)=2x和g(x)=x3的图象的示意图如图所示.设两函数的图象交于点A(x1,y1)、B(x2,y2),且x1<x2.
(1)请指出示意图中曲线C1、C2分别对应哪一个函数?
(2)若x1∈[a,a+1],x2∈[b,b+1],且a、b∈{1,2,3,4,5,6,7,8,9,10,11,12},指出a、b的值,并说明理由;
(3)结合函数图象示意图,请把f(8)、g(8)、f(2012)、g(2012)四个数按从小到大的顺序排列.
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
某同学参加北大、清华、科大三所学校的自主命题招生考试,其被录取的概率分别为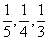 (各 学校是否录取他相互独立,允许他可以被多个学校同时录取).
(各 学校是否录取他相互独立,允许他可以被多个学校同时录取).
(Ⅰ)求此同学没有被任何学校录取的概率;
(Ⅱ)求此同学至少被两所学校录取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=|log2x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m,n的值分别为( )
A.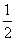 ,2 B.
,2 B.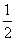 ,4
,4
C.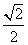 ,
, D.
D.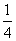 ,4
,4
查看答案和解析>>
科目:高中数学 来源: 题型:
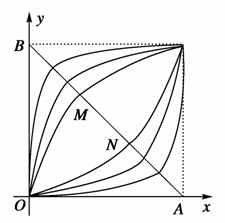
幂函数y=xα(α≠0),当α取不同的正数时,在区间[0,1]上它们的图象是一族美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图象三等分,即有BM=MN=NA.那么,αβ=( )
A.1 B.2 C.3 D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x+2x,g(x)=x+lnx,h(x)=x-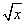 -1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是( )
-1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x1<x3
C.x1<x3<x2 D.x3<x2<x1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=-x2+2ex+m-1,g(x)=x+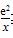 (x>0).
(x>0).
(1)若y=g(x)-m有零点,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
[分析] (1)y=g(x)-m有零点即y=g(x)与y=m的图象有交点,所以可结合图象求解.(2)g(x)-f(x)=0有两个相异实根⇔y=f(x)与y=g(x)的图象有两个不同交点,所以可利用它们的图象求解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com