
分析 (1)分别设甲、乙经第一次选拔后合格为事件A1、B1;设E表示第一次选拔后甲合格、乙不合格,由P(E)=P($\overline{{A}_{1}}$B1),能求出第一次选拔后甲、乙两人中只有乙合格的概率.
(2)分别设甲、乙、丙三人经过前后两次选拔后合格入选为事件A、B、C,由此能够分别求出甲、乙、丙三人经过前后两次选拔后合格的概率.经过前后两次选拔后合格入选的人数为X,则X=0、1、2、3.分别求出P(ξ=0),P(X=1),P(X=2)和PX=2),由此能求出X的概率分布列和Eξ
解答 解:(1)分别设甲、乙经第一次选拔后合格为事件A1、B1,
设E表示第一次选拔后乙合格、甲不合格,
则P(E)=P($\overline{{A}_{1}}$B1)=0.6×0.6=0.36.
(2)分别设甲、乙、丙三人经过前后两次选拔后合格入选为事件A、B、C,
则P(A)=0.4×0.5=0.2,P(B)=0.6×0.5=0.3,P(C)=0.5×0.4=0.2.
经过前后两次选拔后合格入选的人数为X,则X=0、1、2、3.
则P(X=0)=(1-0.2)×(1-0.3)×(1-0.2)=0.448,
P(X=1)=0.2×(1-0.3)(1-0.2)+(1-0.2)×0.3×(1-0.2)+(1-0.2)(1-0.3)×0.2=0.416,
P(X=2)=0.2×0.3×(1-0.2)+0.2×(1-0.3)×0.2+(1-0.2)×0.3×0.2=0.124
P(X=3)=0.2×0.3×0.2=0.012.
∴X的概率分布列为
| X | 0 | 1 | 2 | 3 |
| P | 0.448 | 0.416 | 0.124 | 0.012 |
点评 本题考查概率的计算和离散型随机变量的概率分布列、数学期望的求法,是高考的必考题型.解题时要认真审题,仔细解答,注意合理地进行等价转化.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
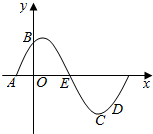 已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)一个周期内的图象上的四个点,如图所示,A(-$\frac{π}{6}$,0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,$\overrightarrow{CD}$在x轴方向上的投影为$\frac{π}{12}$.
已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)一个周期内的图象上的四个点,如图所示,A(-$\frac{π}{6}$,0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,$\overrightarrow{CD}$在x轴方向上的投影为$\frac{π}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1lnx2<x2lnx1 | B. | x1lnx2>x2lnx1 | ||
| C. | x1e${\;}^{{x}_{2}}$<x2e${\;}^{{x}_{1}}$ | D. | x1e${\;}^{{x}_{2}}$>x2e${\;}^{{x}_{1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com