
分析 (1)求出f(x)的导数,可得A,B处的切线方程,代入点(2,t),可得x1,x2为方程t-(-x3+mx2-m)=(-3x2+2mx)(2-x)的两个不等实根,化简整理可得,2x3-(m+6)x2+4mx-m-t=0,令g(x)=2x3-(m+6)x2+4mx-m-t,求出导数,由题意可得g(x)必有一个极值为0,计算即可得到证明;
(2)由题意可得-x3+mx2-m≥-$\frac{1}{2}$x3+mx2+(a+1)x+2xcosx-m,即有$\frac{1}{2}$x3+(a+1)x+2xcosx≤0,讨论x=0,显然成立;当0<x≤1时,运用参数分离和构造函数法,求出导数,判断单调性,求出最值,即可得到所求a的范围.
解答 解:(1)证明:由f($\frac{x}{2}$)=-$\frac{1}{8}$x3+$\frac{m}{4}$x2-m,可得f(x)=-x3+mx2-m,
f′(x)=-3x2+2mx,可得A处的切线方程:y-(-x13+mx12-m)=(-3x12+2mx)(x-x1),
同理可得B处的切线方程:y-(-x23+mx22-m)=(-3x22+2mx)(x-x2),
代入点(2,t),可得x1,x2为方程t-(-x3+mx2-m)=(-3x2+2mx)(2-x)的两个不等实根,
化简整理可得,2x3-(m+6)x2+4mx-m-t=0,
令g(x)=2x3-(m+6)x2+4mx-m-t,g′(x)=6x2-2(m+6)x+4m=2(3x-m)(x-2),
由g′(x)=0,可得x=2或x=$\frac{m}{3}$.
g(2)=3m-8-t,g($\frac{m}{3}$)=-$\frac{1}{27}$m3+$\frac{2}{3}$m2-m-t,
由题意可得g(x)必有一个极值为0,则t=3m-8,或t=-$\frac{1}{27}$m3+$\frac{2}{3}$m2-m;
(2)当x∈[0,1]时,若f(x)≥g(x)恒成立,
即为-x3+mx2-m≥-$\frac{1}{2}$x3+mx2+(a+1)x+2xcosx-m,
即有$\frac{1}{2}$x3+(a+1)x+2xcosx≤0,
当x=0时,上式显然成立;
当0<x≤1时,即有-a-1≥$\frac{1}{2}$x2+2cosx恒成立,
令m(x)=$\frac{1}{2}$x2+2cosx,m′(x)=x-2sinx,m′′(x)=1-2cosx,
由0<x≤1时,1<2cos1≤2cosx<2,则1-2cosx<0,
y=x-2sinx在(0,1]递减,可得x-2sinx<0,
则m(x)在(0,1]递减,可得m(x)<m(0)=2,
则-a-1≥2,解得a≤-3.
a的取值范围是(-∞,-3].
点评 本题考查导数的运用:求切线的方程和不等式恒成立问题解法,注意运用分类讨论的思想方法和转化思想,构造函数法,运用单调性,考查化简整理的运算能力,属于综合题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
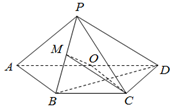 如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{1}{12},-\frac{4}{49})$ | B. | $[-\frac{1}{12},0]$ | C. | $(-\frac{4}{49},0]$ | D. | $[-\frac{4}{49},0]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )
球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )| A. | $\frac{4π}{3}$ | B. | 4π | C. | 12π | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
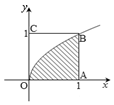 如图,在正方形OABC内任取一点,取到函数$y=\sqrt{x}$的图象与x轴正半轴之间
如图,在正方形OABC内任取一点,取到函数$y=\sqrt{x}$的图象与x轴正半轴之间查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com