若双曲线
－
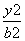＝1(a>0，b>0)与直线y＝
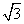x无交点，则离心率e的取值范围是( )
A．(1,2) B．(1,2]
C．(1，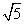
) D．(1，]
名师指导期末冲刺卷系列答案
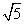开心蛙口算题卡系列答案科目：高中数学 来源： 题型：
已知：圆C：x2＋y2－8y＋12＝0，直线l：ax＋y＋2a＝0.
(1)当a为何值时，直线l与圆C相切；
(2)当直线l与圆C相交于A，B两点，且|AB|＝2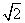
时，求直线l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知抛物线y2＝2px(p>0)的焦点弦AB的两端点坐标分别为A(x1，y1)，B(x2，y2)，则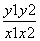
的值一定等于( )
A．－4 B．4
C．p2 D．－p2
查看答案和解析>>
科目：高中数学 来源： 题型：
已知动圆过定点A(0,2)，且在x轴上截得的弦长为4.
(1)求动圆圆心的轨迹C的方程；
(2)点P为轨迹C上任意一点，直线l为轨迹C上在点P处的切线，直线l交直线：y＝－1于点R，过点P作PQ⊥l交轨迹C于点Q，求△PQR的面积的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知直线l：y＝x＋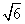
，圆O：x2＋y2＝5，椭圆E：
＋
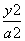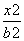＝1(a>b>0)的离心率e＝
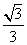，直线l被圆O截得的弦长与椭圆的短轴长相等．
(1)求椭圆E的方程；
(2)过圆O上任意一点P作椭圆E的两条切线，若切线都存在斜率，求证：两切线斜率之积为定值．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知椭圆C过点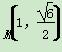
，点F(－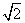
，0)是椭圆的左焦点，点P，Q是椭圆C上的两个动点，且|PF|，|MF|，|QF|成等差数列．
(1)求椭圆C的标准方程；
(2)求证：线段PQ的垂直平分线经过一个定点A.
查看答案和解析>>
科目：高中数学 来源： 题型：
在“世界读书日”前夕，为了了解某地5 000名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析．在这个问题中，5 000名居民的阅读时间的全体是( )
A．总体
B．个体
C．样本的容量
D．从总体中抽取的一个样本
查看答案和解析>>
科目：高中数学 来源： 题型：
为了调查某大学学生在某天上网的时间，随机对100名男生和100名女生进行了不记名的问卷调查．得到了如下的统计结果：
表1：男生上网时间与频数分布表
| 上网时间 (分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
表2：女生上网时间与频数分布表
| 上网时间 (分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
(1)从这100名男生中任意选出3人，求其中恰有1人上网时间少于60分钟的概率；
(2)完成下面的2×2列联表，并回答能否有90%的把握认为“大学生上网时间与性别有关”？
|
| 上网时间少 于60分钟 | 上网时间不少 于60分钟 | 合计 |
| 男生 | |||
| 女生 | |||
| 合计 |
附：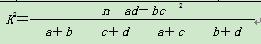
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
