
分析 对a进行分类讨论,求出不等式的解集,再根据,关于x的不等式ax2-4ax-2>0的解集与集合{x|3<x<4}的交集不空,列出满足的条件即可求实数a的取值范围.
解答 解:当a=0,-2>0不成立,不符合要求;
当a≠0时,关于x的不等式ax2-4ax-2>0的解集与集合{x|3<x<4}的交集不空,
所以对于方程ax2-4ax-2=0的△=16a2+8a≥0,解得a>0或a≤-$\frac{1}{2}$,
所以方程的根为x=$\frac{2a-\sqrt{4{a}^{2}+2a}}{a}$或x=$\frac{2a+\sqrt{4{a}^{2}+2a}}{a}$
当a>0时,不等式的ax2-4ax-2>0的解集为{x|x<$\frac{2a-\sqrt{4{a}^{2}+2a}}{a}$或x>$\frac{2a+\sqrt{4{a}^{2}+2a}}{a}$},
∴$\frac{2a+\sqrt{4{a}^{2}+2a}}{a}$<4,
解得a<0,(舍去),
当a≤-$\frac{1}{2}$时,不等式的ax2-4ax-2>0的解集为{x|$\frac{2a-\sqrt{4{a}^{2}+2a}}{a}$<x<$\frac{2a+\sqrt{4{a}^{2}+2a}}{a}$},
∵$\frac{2a-\sqrt{4{a}^{2}+2a}}{a}$>0,$\frac{2a+\sqrt{4{a}^{2}+2a}}{a}$>4,
∴$\frac{2a-\sqrt{4{a}^{2}+2a}}{a}$>3,
解得a<-$\frac{2}{3}$,
综上所述a的取值范围为(-∞,-$\frac{2}{3}$)
点评 本题是对二次函数的图象所在位置的考查.其中涉及到对二次项系数的讨论,在做题过程中,只要二次项系数含参数,就要分情况讨论,这也是本题的一个易错点.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
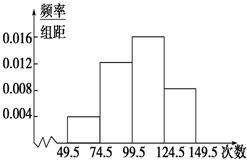 为了了解学生的体能情况,抽取了某学校同年级部分学生作为样本进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第四小组的频数为10.
为了了解学生的体能情况,抽取了某学校同年级部分学生作为样本进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第四小组的频数为10.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com