
分析 作出f(x)和y=ax的函数图象,根据图象及交点个数得出a的范围.
解答 解:f(x)=$\left\{\begin{array}{l}{x+1,x<0}\\{1-x,0≤x≤1}\\{-lnx,x>1}\end{array}\right.$,
作出y=f(x)的函数图象如图所示: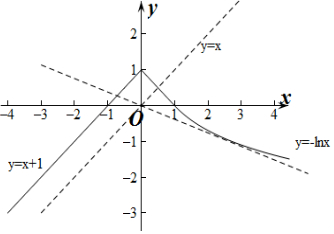
设直线y=ax与y=-lnx相切,切点为(x0,y0),
则$\left\{\begin{array}{l}{{y}_{0}=a{x}_{0}}\\{{y}_{0}=-ln{x}_{0}}\\{-\frac{1}{{x}_{0}}=a}\end{array}\right.$,解得x0=e,y0=-1,a=-$\frac{1}{e}$.
∵f(x)-ax=0只有一解,
∴y=f(x)与y=ax的函数图象只有1个交点,
∴a≥1或a<-$\frac{1}{e}$.
故答案为:(-∞,-$\frac{1}{e}$)∪[1,+∞).
点评 本题考查了方程解与函数图象的关系,属于中档题.


科目:高中数学 来源: 题型:解答题
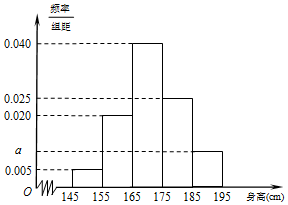 某中学随机选取了40名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.
某中学随机选取了40名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | a<c<b | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com