
分析 (1)求出原函数的导函数,再令h(x)=alnx+$\frac{1}{x}$,求其导函数可得h(x)在(0,$\frac{1}{a}$)上单调递减,在($\frac{1}{a},+∞$)上单调递增,由f(x)在定义域内单调递增,
则h($\frac{1}{a}$)≥0,由此求得实数a的取值范围;
(2)由(1)可得g(x)=h(x),$\frac{1}{a}$是g(x)的极小值点.不妨设0$<{x}_{1}<\frac{1}{a}<{x}_{2}$,令φ(x)=g(x)-g($\frac{2}{a}-x$)(0$<x<\frac{1}{a}$),可得φ′(x)<0.由此φ(x)>φ($\frac{1}{a}$)=0,得到g(x)>g($\frac{2}{a}-x$)(0$<x<\frac{1}{a}$).代入x=x1,得g(x2)=g(x1)>g($\frac{2}{a}-{x}_{1}$),由g(x)在($\frac{1}{a},+∞$)上单调递增得答案.
解答 (1)解:$f′(x)={e}^{ax}(alnx+\frac{1}{x})$,令h(x)=alnx+$\frac{1}{x}$,则h′(x)=$\frac{ax-1}{{x}^{2}}$,
令h′(x)=0,得x=$\frac{1}{a}$.
∴h(x)在(0,$\frac{1}{a}$)上单调递减,在($\frac{1}{a},+∞$)上单调递增,要使f(x)在定义域内单调递增,
则h($\frac{1}{a}$)≥0,即a(ln$\frac{1}{a}$+1)≥0,解得:a∈(0,e];
(2)证明:g(x)=$\frac{f′(x)}{{e}^{ax}}$=h(x),由(1)知,$\frac{1}{a}$是g(x)的极小值点.
不妨设0$<{x}_{1}<\frac{1}{a}<{x}_{2}$,令φ(x)=g(x)-g($\frac{2}{a}-x$)(0$<x<\frac{1}{a}$),
则φ′(x)=g′(x)-g′($\frac{2}{a}-x$)=$\frac{ax-1}{{x}^{2}}-(-1)×\frac{a(\frac{2}{a}-x)-1}{(\frac{2}{a}-x)^{2}}$=$-\frac{4(ax-1)^{2}}{{x}^{2}(2-ax)^{2}}<0$.
由此φ(x)>φ($\frac{1}{a}$)=0,即g(x)>g($\frac{2}{a}-x$)(0$<x<\frac{1}{a}$).代入x=x1 得:g(x2)=g(x1)>g($\frac{2}{a}-{x}_{1}$),
由g(x)在($\frac{1}{a},+∞$)上单调递增,因此${x}_{2}>\frac{2}{a}-{x}_{1}$,
∴x1+x2>$\frac{2}{a}$.
点评 本题考查利用导数研究函数的单调性,考查了利用导数求函数的极值,考查逻辑推理能力与运算能力,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | y=-$\frac{1}{x}$ | B. | y=log2(x-1) | ||
| C. | y=$\left\{\begin{array}{l}{{3}^{x},x≥0}\\{-{3}^{-x},x<0}\end{array}\right.$ | D. | y=ln(x+$\sqrt{{x}^{2}+1}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{9}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1000 | B. | 600 | C. | 550 | D. | 500 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{5}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
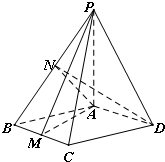 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点..
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com