
设A,B分别是直线y=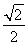 x和y=-
x和y=-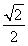 x上的动点,且|AB|=
x上的动点,且|AB|=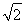 ,设O为坐标原点,动点P满足
,设O为坐标原点,动点P满足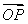 =
=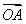 +
+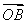 .
.
(1)求点P的轨迹方程;
(2)过点(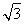 ,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
(1)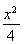 +y2=1(2)见解析
+y2=1(2)见解析
【解析】(1)设A(x1,y1),B(x2,y2),P(x,y),
∵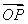 =
=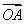 +
+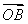 ,∴x=x1+x2,y=y1+y2,
,∴x=x1+x2,y=y1+y2,
∵y1=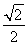 x1,y2=-
x1,y2=-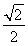 x2,?
x2,?
∴x=x1+x2=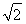 (y1-y2),y=y1+y2=
(y1-y2),y=y1+y2=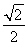 (x1-x2).
(x1-x2).
∵|AB|=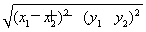 =
=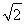 ,∴
,∴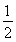 x2+2y2=2,
x2+2y2=2,
∴点P的轨迹方程为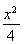 +y2=1.
+y2=1.
(2)证明:设C(x1,y1),D(x2,y2),直线l1的方程为x-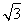 =ky.
=ky.
由 ,得(k2+4)y2+2
,得(k2+4)y2+2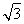 ky-1=0,
ky-1=0,
∴y1+y2=-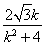 ,x1+x2=
,x1+x2=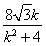 .∴M点坐标为
.∴M点坐标为 ,
,
同理可得N点坐标为 .
.
∴直线MN的斜率kMN= .
.
∴直线MN的方程为y+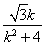 =
=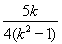
 .
.
整理化简得4k4y+(4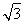 -5x)k3+12k2y-16y+(-20x+16
-5x)k3+12k2y-16y+(-20x+16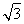 )k=0,
)k=0,
∴x=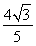 ,y=0,∴直线MN恒过定点
,y=0,∴直线MN恒过定点


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练4练习卷(解析版) 题型:选择题
已知向量a,b是夹角为60°的两个单位向量,向量a+λb(λ∈R)与向量a-2b垂直,则实数λ的值为( )
A.1 B.-1 C.2 D.0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练1练习卷(解析版) 题型:选择题
若变量x,y满足约束条件 且z=5y-x的最大值为a,最小值为b,则a-b的值是( )
且z=5y-x的最大值为a,最小值为b,则a-b的值是( )
A.48 B.30
C.24 D.16
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题6第2课时练习卷(解析版) 题型:选择题
已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=( )

A.0.6 B.0.4 C.0.3 D.0.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题6第1课时练习卷(解析版) 题型:填空题
某数学老师身高176 cm,他爷爷、父亲和儿子的身高分别是173 cm、170 cm和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第2课时练习卷(解析版) 题型:解答题
已知椭圆M: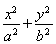 =1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
=1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.
(1)求椭圆M的方程;
(2)设直线l:x=my+t与椭圆M交于A,B两点,若以AB为直径的圆经过椭圆的右顶点C,求t的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第2课时练习卷(解析版) 题型:选择题
已知P为双曲线C: =1上的点,点M满足|
=1上的点,点M满足| 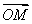 |=1,且
|=1,且 ·
· =0,则当|
=0,则当|  |取得最小值时的点P到双曲线C的渐近线的距离为( )
|取得最小值时的点P到双曲线C的渐近线的距离为( )
A. B.
B.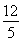 C.4 D.5
C.4 D.5
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第3课时练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4 ,AB=2CD=8.
,AB=2CD=8.

(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
(3)求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:选择题
已知等差数列{an}的前n项和为Sn,a4=15,S5=55,则数列{an}的公差是( )
A. B.4 C.-4 D.-3
B.4 C.-4 D.-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com