
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4 ,AB=2CD=8.
,AB=2CD=8.

(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
(3)求四棱锥P-ABCD的体积.
(1)见解析(2)M点位于线段PC靠近C点的三等分点处时(3)24.
【解析】(1)证明:在△ABD中,
∵AD=4,BD=4 ,AB=8,∴AD2+BD2=AB2.
,AB=8,∴AD2+BD2=AB2.
∴AD⊥BD.
又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,BD?平面ABCD,
∴BD⊥平面PAD.
又BD?平面MBD,∴平面MBD⊥平面PAD.
(2)当M点位于线段PC靠近C点的三等分点处时,
PA∥平面MBD.
证明如下:连接AC,交BD于点N,连接MN.
∵AB∥DC,∴四边形ABCD是梯形.
∵AB=2CD,
∴CN∶NA=1∶2.
又∵CM∶MP=1∶2,∴CN∶NA=CM∶MP,∴PA∥MN.
∵MN?平面MBD,PA?平面MBD,∴PA∥平面MBD.
(3)过点P作PO⊥AD交AD于O,
∵平面PAD⊥平面ABCD,∴PO⊥平面ABCD.
即PO为四棱锥P-ABCD的高.
又△PAD是边长为4的等边三角形,∴PO=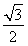 ×4=2
×4=2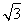 .
.
在Rt△ADB中,斜边AB上的高为 =2
=2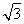 ,此即为梯形ABCD的高.
,此即为梯形ABCD的高.
梯形ABCD的面积SABCD=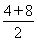 ×2
×2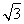 =12
=12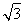 .
.
四棱锥P-ABCD的体积VP-ABCD=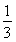 ×12
×12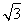 ×2
×2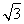 =24.
=24.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练2练习卷(解析版) 题型:选择题
已知双曲线的一个焦点与抛物线x2=20y的焦点重合,且其渐近线的方程为3x±4y=0,则该双曲线的标准方程为( )
A. =1 B.
=1 B.  =1
=1
C.  =1 D.
=1 D.  =1
=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第3课时练习卷(解析版) 题型:解答题
设A,B分别是直线y=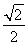 x和y=-
x和y=-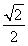 x上的动点,且|AB|=
x上的动点,且|AB|=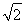 ,设O为坐标原点,动点P满足
,设O为坐标原点,动点P满足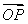 =
=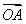 +
+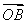 .
.
(1)求点P的轨迹方程;
(2)过点(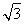 ,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第1课时练习卷(解析版) 题型:解答题
如图所示,已知直线l:y=x,圆C1的圆心为(3,0),且经过点A(4,1).
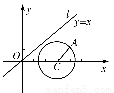
(1)求圆C1的方程;
(2)若圆C2与圆C1关于直线l对称,点B、D分别为圆C1、C2上任意一点,求|BD|的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第1课时练习卷(解析版) 题型:选择题
已知圆心(a,b)(a<0,b<0)在直线y=2x+1上的圆,其圆心到x轴的距离恰好等于圆的半径,在y轴上截得的弦长为2 ,则圆的方程为( )
,则圆的方程为( )
A.(x+2)2+(y+3)2=9 B.(x+3)2+(y+5)2=25
C.(x+6)2+ 2=
2= D.
D. 2+
2+ 2=
2=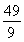
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第2课时练习卷(解析版) 题型:解答题
已知四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.

(1)求证:BE∥平面PDA;
(2)若N为线段PB的中点,求证:NE⊥平面PDB.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第2课时练习卷(解析版) 题型:选择题
已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定( )
A.与a,b都相交
B.只能与a,b中的一条相交
C.至少与a,b中的一条相交
D.与a,b都平行
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第3课时练习卷(解析版) 题型:解答题
某工业城市按照“十二五”(2011年至2015年)期间本地区主要污染物排放总量控制要求,进行减排治污.现以降低SO2的年排放量为例,原计划“十二五”期间每年的排放量都比上一年减少0.3万吨,已知该城市2011年SO2的年排放量约为9.3万吨.
(1)按原计划,“十二五”期间该城市共排放SO2约多少万吨?
(2)该城市为响应“十八大”提出的建设“美丽中国”的号召,决定加大减排力度.在2012年刚好按原计划完成减排任务的条件下,自2013年起,SO2的年排放量每年比上一年减少的百分率为p,为使2020年这一年SO2的年排放量控制在6万吨以内,求p的取值范围.
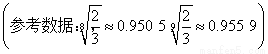
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
下面是关于复数z=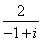 的四个命题:
的四个命题:
p1:|z|=2,p2:z2=2i,
p3:z的共轭复数为1+i,p4:z的虚部为-1.
其中的真命题为( )
A.p1,p3 B.p1,p2
C.p2,p4 D.p3,p4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com