
已知四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.

(1)求证:BE∥平面PDA;
(2)若N为线段PB的中点,求证:NE⊥平面PDB.
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第2课时练习卷(解析版) 题型:解答题
已知椭圆M: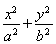 =1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
=1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.
(1)求椭圆M的方程;
(2)设直线l:x=my+t与椭圆M交于A,B两点,若以AB为直径的圆经过椭圆的右顶点C,求t的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第1课时练习卷(解析版) 题型:选择题
若实数x,y满足x|x|-y|y|=1,则点(x,y)到直线y=x的距离的取值范围是( )
A.[1,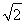 ) B.(0,
) B.(0, ] C.
] C.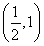 D.(0,1]
D.(0,1]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第3课时练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4 ,AB=2CD=8.
,AB=2CD=8.

(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
(3)求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第2课时练习卷(解析版) 题型:选择题
已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的有( )
A.若m∥α,n∥α,则m∥n B.若α⊥γ,β⊥γ,则α∥β
C.若m∥α,m∥β,则α∥β D.若m⊥α,n⊥α,则m∥n
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第1课时练习卷(解析版) 题型:解答题
一个几何体的三视图如下图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为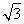 ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
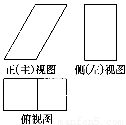
(1)求该几何体的体积V;
(2)求该几何体的表面积S.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:填空题
若数列{an}的前n项和Sn=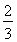 an+
an+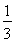 ,则{an}的通项公式是an=________.
,则{an}的通项公式是an=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
已知i为虚数单位,复数z=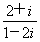 ,则|z|+
,则|z|+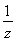 =( )
=( )
A.i B.1-I C.1+i D.-i
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com