
某工业城市按照“十二五”(2011年至2015年)期间本地区主要污染物排放总量控制要求,进行减排治污.现以降低SO2的年排放量为例,原计划“十二五”期间每年的排放量都比上一年减少0.3万吨,已知该城市2011年SO2的年排放量约为9.3万吨.
(1)按原计划,“十二五”期间该城市共排放SO2约多少万吨?
(2)该城市为响应“十八大”提出的建设“美丽中国”的号召,决定加大减排力度.在2012年刚好按原计划完成减排任务的条件下,自2013年起,SO2的年排放量每年比上一年减少的百分率为p,为使2020年这一年SO2的年排放量控制在6万吨以内,求p的取值范围.
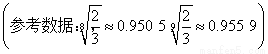
(1)43.5万吨(2)4.95%<p<1
【解析】(1)设“十二五”期间,该城市共排放SO2约y万吨,依题意,2011年至2015年SO2的年排放量构成首项为9.3,公差为-0.3的等差数列,
所以y=5×9.3+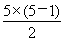 ×(-0.3)=43. 5(万吨).
×(-0.3)=43. 5(万吨).
所以按原计划“十二五”期间该城市共排放SO2约43.5万吨.
(2)由已知得,2012年的SO2年排放量为9.3-0.3=9(万吨),
所以2012年至2020年SO2的年排放量构成首项为9,公比为1-p的等比数列.
由题意得9×(1-p)8<6,由于0<p<1,所以1-p<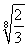 ,所以1-p<0.950 5,解得p>4.95%.
,所以1-p<0.950 5,解得p>4.95%.
所以SO2的年排放量每年减少的百分率p的取值范围为4.95%<p<1


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题6第2课时练习卷(解析版) 题型:选择题
已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=( )

A.0.6 B.0.4 C.0.3 D.0.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第3课时练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4 ,AB=2CD=8.
,AB=2CD=8.

(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
(3)求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第1课时练习卷(解析版) 题型:解答题
一个几何体的三视图如下图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为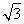 ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
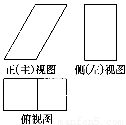
(1)求该几何体的体积V;
(2)求该几何体的表面积S.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第1课时练习卷(解析版) 题型:选择题
已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V1,直径为4的球的体积为V2,则( )

A.1∶2 B.2∶1 C.1∶1 D.1∶4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:填空题
若数列{an}的前n项和Sn=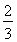 an+
an+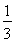 ,则{an}的通项公式是an=________.
,则{an}的通项公式是an=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:选择题
已知等差数列{an}的前n项和为Sn,a4=15,S5=55,则数列{an}的公差是( )
A. B.4 C.-4 D.-3
B.4 C.-4 D.-3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:填空题
已知向量a=(m,n),b=(p,q),定义a?b=mn-pq.给出下列四个结论:①a?a=0;②a?b=b?a;③(a+b)?a=a?a+b?a;④(a?b)2+(a·b)2=(m2+q2)·(n2+p2).
其中正确的结论是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:选择题
已知sin α-cos α=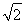 ,α∈(0,π),则tan α=( )
,α∈(0,π),则tan α=( )
A.-1 B.-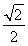 C.
C.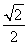 D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com