
| 男生 | 93 | 91 | 90 | 86 | 83 | 80 | 76 | 69 | 67 | 65 |
| 女生 | 96 | 87 | 85 | 83 | 79 | 78 | 77 | 74 | 73 | 68 |
分析 (Ⅰ)由两组数据能完成男、女生成绩的茎叶图,并能求出男生的平均成绩和女生的平均成绩,由茎叶图可以看出,男生的成绩比较分散,女生的成绩比较集中.
(Ⅱ)成绩在80分以上(包括80分)的学生共有10人,其中男生6人,女生4人,X的所有可能取值为-2,0,2,分别求出相应的概率,由此能求出X的数学期望.
解答 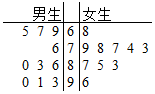 解:(Ⅰ)由两组数据完成男、女生成绩的茎叶图,如下图所示.
解:(Ⅰ)由两组数据完成男、女生成绩的茎叶图,如下图所示.
(2分)
男生的平均成绩为$\overline x=\frac{1}{10}(3×90+3×80+70+3×60+1+3+3+6+6+5+7+9)=80$,
女生的平均成绩为$\overline y=\frac{1}{10}(90+3×80+5×70+60+6+7+5+3+9+8+7+4+3+8)=80$,
∴男、女生的平均成绩一样.(5分)
由茎叶图可以看出,男生的成绩比较分散,女生的成绩比较集中.(6分)
(Ⅱ)成绩在80分以上(包括80分)的学生共有10人,其中男生6人,女生4人,
X的所有可能取值为-2,0,2,(7分)
$P(X=-2)=\frac{C_6^1C_4^3}{C_6^1C_4^3+C_6^2C_4^2+C_6^3C_4^1}=\frac{12}{97}$,(8分)
$P(X=0)=\frac{C_6^2C_4^2}{C_6^1C_4^3+C_6^2C_4^2+C_6^3C_4^1}=\frac{45}{97}$,(9分)
$P(X=2)=\frac{C_6^3C_4^1}{C_6^1C_4^3+C_6^2C_4^2+C_6^3C_4^1}=\frac{40}{97}$,(10分)
∴$E(X)=-2×\frac{12}{97}+0×\frac{45}{97}+2×\frac{40}{97}=\frac{56}{97}$.(12分)
点评 本小题主要考查茎叶图的画法和理解,古典概型,随机变量的数学期望等基础知识,考查运算求解能力、数据处理能力、应用意识,考查必然与或然思想、化归与转化思想.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人及5人以上 |
| 概率 | 0.05 | 0.14 | 0.35 | 0.3 | 0.1 | 0.06 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某城市要建宜居的新城,准备引进优秀企业进行城市建设.这个城市的甲区、乙区分别对6个企业进行评估,综合得分情况如茎叶图所示.
某城市要建宜居的新城,准备引进优秀企业进行城市建设.这个城市的甲区、乙区分别对6个企业进行评估,综合得分情况如茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也可称为可入肺颗粒物,我国规定PM2.5的数值在0~50ug/m2为空气质量一等,甲、乙两城市现参加全国“空气质量优秀城市”评选,下表是2011至2015年甲乙两市空气质量一等天数的记录(单位:天):
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也可称为可入肺颗粒物,我国规定PM2.5的数值在0~50ug/m2为空气质量一等,甲、乙两城市现参加全国“空气质量优秀城市”评选,下表是2011至2015年甲乙两市空气质量一等天数的记录(单位:天):| 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | |
| 甲 | 86 | 77 | 92 | 72 | 78 |
| 乙 | 78 | 82 | 88 | 82 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
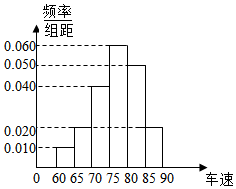 2016年“五一”期间,高速公路某服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽查一辆进行询问调查.共询问调查40名驾驶员.将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),
2016年“五一”期间,高速公路某服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽查一辆进行询问调查.共询问调查40名驾驶员.将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com