
分析 (Ⅰ)记“甲第i次抢得红包”为事件Ai(i=1,2),“甲第i次没有抢得红包”为事件$\overline{A_i}$.记“甲恰有1次抢得红包”为事件A,则$A={A_1}\overline{A_2}+\overline{A_1}{A_2}$,由此利用事件的独立性和互斥性,能求出甲恰有1次抢得红包的概率.
(2)记“乙第i次抢得红包”为事件Bi(i=1,2,3),“乙第i次没有抢得红包”为事件$\overline{B_i}$.由题意知X的所有可能取值为0,5,10,15,20,由事件的独立性和互斥性,分别求出相应的概率,由此能求出
X的分布列和数学期望.
解答 解:(Ⅰ)记“甲第i次抢得红包”为事件Ai(i=1,2),“甲第i次没有抢得红包”为事件$\overline{A_i}$.
则$P({A_i})=\frac{1}{3}$,$P(\overline{A_i})=\frac{2}{3}$.(1分)
记“甲恰有1次抢得红包”为事件A,则$A={A_1}\overline{A_2}+\overline{A_1}{A_2}$,(2分)
由事件的独立性和互斥性,得$P(A)=P({A_1}\overline{A_2}+\overline{A_1}{A_2})=P({A_1}\overline{A_2})+P(\overline{A_1}{A_2})=P({A_1})P(\overline{A_2})+P(\overline{A_1})P({A_2})$(3分)
=$\frac{1}{3}×\frac{2}{3}+\frac{2}{3}×\frac{1}{3}=\frac{4}{9}$.(4分)
(2)记“乙第i次抢得红包”为事件Bi(i=1,2,3),“乙第i次没有抢得红包”为事件$\overline{B_i}$.
则$P({B_i})=\frac{1}{3}$,$P(\overline{B_i})=\frac{2}{3}$.
由题意知X的所有可能取值为0,5,10,15,20,(5分)
由事件的独立性和互斥性,得:
$P(X=0)=P(\overline{B_1}\overline{B_2}\overline{B_3})={(\frac{2}{3})^3}=\frac{8}{27}$.(6分)
$P(X=5)=P({B_1}\overline{B_2}\overline{B_3}+\overline{B_1}{B_2}\overline{B_3})=2×\frac{1}{3}×{(\frac{2}{3})^2}=\frac{8}{27}$.(7分)
$P(X=10)=P({B_1}{B_2}\overline{B_3}+\overline{B_1}\overline{B_2}{B_3})={(\frac{1}{3})^2}×\frac{2}{3}+{(\frac{2}{3})^2}×\frac{1}{3}=\frac{2}{9}$.(8分)
$P(X=15)=P({B_1}\overline{B_2}{B_3}+\overline{B_1}{B_2}{B_3})=2×{(\frac{1}{3})^2}×\frac{2}{3}=\frac{4}{27}$.(9分)
$P(X=20)=P({B_1}{B_2}{B_3})={(\frac{1}{3})^3}=\frac{1}{27}$.(10分)
所以X的分布列为:
| X | 0 | 5 | 10 | 15 | 20 |
| P | $\frac{8}{27}$ | $\frac{8}{27}$ | $\frac{2}{9}$ | $\frac{4}{27}$ | $\frac{1}{27}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意事件的独立性和互斥性的合理运用.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [-18,6] | B. | [6-5$\sqrt{2}$,6+5$\sqrt{2}$] | C. | [-16,4] | D. | [-6-5$\sqrt{2}$,-6+5$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男生 | 93 | 91 | 90 | 86 | 83 | 80 | 76 | 69 | 67 | 65 |
| 女生 | 96 | 87 | 85 | 83 | 79 | 78 | 77 | 74 | 73 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 反对 | 合计 | |
| 教师 | 16 | 14 | 30 |
| 学生 | 44 | 26 | 70 |
| 合计 | 60 | 40 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
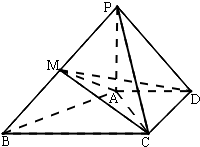 在四棱锥P-ABCD中,AD∥BC,DC⊥AD,PA⊥平面ABCD,2AD=BC=2$\sqrt{3}$,∠DAC=30°,M为PB中点.
在四棱锥P-ABCD中,AD∥BC,DC⊥AD,PA⊥平面ABCD,2AD=BC=2$\sqrt{3}$,∠DAC=30°,M为PB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com