
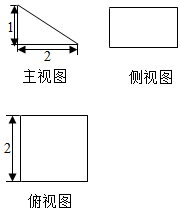
 某空间几何体的三视图如图所示,则该几何体的外接球表面积为9π.
某空间几何体的三视图如图所示,则该几何体的外接球表面积为9π. 科目:高中数学 来源: 题型:解答题
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人及5人以上 |
| 概率 | 0.05 | 0.14 | 0.35 | 0.3 | 0.1 | 0.06 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
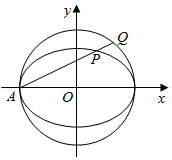 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
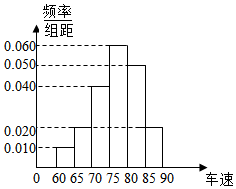 2016年“五一”期间,高速公路某服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽查一辆进行询问调查.共询问调查40名驾驶员.将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),
2016年“五一”期间,高速公路某服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽查一辆进行询问调查.共询问调查40名驾驶员.将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com