
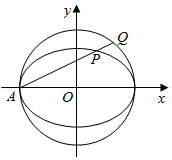
 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.分析 (1)由题意可得a=2,运用离心率公式和a,b,c的关系可得b,c,进而得到椭圆方程和圆的方程,设出直线l的方程代入椭圆方程,求得弦长AP,运用圆的弦长公式可AQ,进而所求之比;或联立直线的方程和椭圆方程(或圆的方程)求得P,Q的纵坐标,即可得到所求之比;
(2)若$\overrightarrow{PQ}=λ\overrightarrow{AP}$,则$λ=\frac{AQ}{AP}-1$,设直线l:y=k(x+2),代入椭圆方程,求得交点,以及弦长AP,代入圆方程可得交点,可得弦长AQ,可得实数λ的式子,运用不等式的性质即可得到所求范围;或将直线方程代入椭圆方程(圆方程)求得P,Q的纵坐标,由坐标之比,结合不等式的性质,即可得到所求范围.
解答 解:(1)由条件可得,2a=4,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a2-b2=c2,
解得a=2,b=c=$\sqrt{2}$,
可得椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$,圆的方程为x2+y2=4;
(方法一)直线l的方程为$y=\frac{1}{2}({x+2})$,由$\left\{\begin{array}{l}y=\frac{1}{2}({x+2})\\{x^2}+2{y^2}=4\end{array}\right.$得:3x2+4x-4=0,
解得${x_A}=-2,{x_p}=\frac{2}{3}$,所以$P({\frac{2}{3},\frac{4}{3}})$;
所以$AP=\sqrt{{{({\frac{2}{3}+2})}^2}+{{({\frac{4}{3}})}^2}}=\frac{{4\sqrt{5}}}{3}$,又因为原点O到直线l的距离$d=\frac{2}{{\sqrt{5}}}$,
所以$AQ=2\sqrt{4-\frac{4}{5}}=\frac{{8\sqrt{5}}}{5}$,
所以$\frac{AP}{AQ}=\frac{{\frac{{4\sqrt{5}}}{3}}}{{\frac{{8\sqrt{5}}}{5}}}=\frac{5}{6}$;
(方法二)由$\left\{\begin{array}{l}x=2y-2\\{x^2}+2{y^2}=4\end{array}\right.$得3y2-4y=0,所以yP=$\frac{4}{3}$,
由$\left\{\begin{array}{l}{x=2y-2}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$可得5y2-8y=0,解得yQ=$\frac{8}{5}$,
所以$\frac{AP}{AQ}$=$\frac{{y}_{P}}{{y}_{Q}}$=$\frac{4}{3}$×$\frac{5}{8}$=$\frac{5}{6}$;
(2)(方法一)若$\overrightarrow{PQ}=λ\overrightarrow{AP}$,则$λ=\frac{AQ}{AP}-1$,
设直线l:y=k(x+2),由$\left\{\begin{array}{l}{x^2}+2{y^2}=4\\ y=k({x+2})\end{array}\right.$得,(2k2+1)x2+8k2-4=0,
即(x+2)[(2k2+1)x+(4k2-2)]=0,
所以${x_A}=-2,{x_P}=\frac{{2-4{k^2}}}{{2{k^2}+1}}$,得$P({\frac{{2-4{k^2}}}{{2{k^2}+1}},\frac{4k}{{2{k^2}+1}}})$;
所以$A{P^2}={({\frac{{2-4{k^2}}}{{2{k^2}+1}}+2})^2}+{({\frac{4k}{{2{k^2}+1}}})^2}=\frac{{16+16{k^2}}}{{{{({2{k^2}+1})}^2}}}$,
即$AP=\frac{{4\sqrt{{k^2}+1}}}{{2{k^2}+1}}$,同理Q($\frac{2-2{k}^{2}}{1+{k}^{2}}$,$\frac{4k}{1+{k}^{2}}$),$AQ=\frac{4}{{\sqrt{{k^2}+1}}}$,
即有λ=$\frac{\frac{4}{\sqrt{{k}^{2}+1}}}{\frac{4\sqrt{{k}^{2}+1}}{2{k}^{2}+1}}$-1=1-$\frac{1}{1+{k}^{2}}$,
由k2>0,可得0<k2<1.
(方法二)由方法一可得,λ=$\frac{AQ}{AP}$-1=$\frac{{y}_{Q}}{{y}_{P}}$-1=$\frac{\frac{4k}{{k}^{2}+1}}{\frac{4k}{2{k}^{2}+1}}$-1=1-$\frac{1}{1+{k}^{2}}$,
由题意:k2>0,所以0<λ<1.
点评 本题考查椭圆的方程和圆的方程的求法,注意运用离心率公式,考查弦长之比,注意运用弦长公式和向量的坐标之比,考查向量共线的坐标以及化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-18,6] | B. | [6-5$\sqrt{2}$,6+5$\sqrt{2}$] | C. | [-16,4] | D. | [-6-5$\sqrt{2}$,-6+5$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
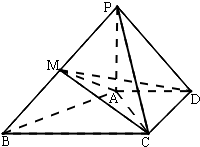 在四棱锥P-ABCD中,AD∥BC,DC⊥AD,PA⊥平面ABCD,2AD=BC=2$\sqrt{3}$,∠DAC=30°,M为PB中点.
在四棱锥P-ABCD中,AD∥BC,DC⊥AD,PA⊥平面ABCD,2AD=BC=2$\sqrt{3}$,∠DAC=30°,M为PB中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某重点高中拟把学校打造成新型示范高中,为此规定了很多新的规章制度.新规章制度实施一段时间后,学校就新规章制度的认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问题5分,调查结束后,按成绩分成5组;第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,已知甲,乙两人同在第3组,丙,丁两人分别在第4,5组,现在用分层抽样的方法在第3,4,5组共选取6人,进行强化培训.
某重点高中拟把学校打造成新型示范高中,为此规定了很多新的规章制度.新规章制度实施一段时间后,学校就新规章制度的认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问题5分,调查结束后,按成绩分成5组;第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,已知甲,乙两人同在第3组,丙,丁两人分别在第4,5组,现在用分层抽样的方法在第3,4,5组共选取6人,进行强化培训.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com