
| A. | [-18,6] | B. | [6-5$\sqrt{2}$,6+5$\sqrt{2}$] | C. | [-16,4] | D. | [-6-5$\sqrt{2}$,-6+5$\sqrt{2}$] |
分析 由切线的对称性和圆的知识将问题转化为C(2,0)到直线l的距离小于或等于2,再由点到直线的距离公式得到关于a的不等式求解.
解答 解:圆C:(x-2)2+y2=2,圆心为:(2,0),半径为$\sqrt{2}$,
∵在直线l上存在一点M,使得过M的圆C的切线MP,MQ(P,Q为切点)满足∠PMQ=90°,
∴在直线l上存在一点M,使得M到C(2,0)的距离等于2,
∴只需C(2,0)到直线l的距离小于或等于2,
故$\frac{|3×2+4×0+a|}{\sqrt{{3}^{2}+{4}^{2}}}≤$2,解得-16≤a≤4,
故选:C.
点评 本题考查直线和圆的位置关系,由题意得到圆心到直线的距离小于或等于2是解决问题的关键,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人及5人以上 |
| 概率 | 0.05 | 0.14 | 0.35 | 0.3 | 0.1 | 0.06 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某城市要建宜居的新城,准备引进优秀企业进行城市建设.这个城市的甲区、乙区分别对6个企业进行评估,综合得分情况如茎叶图所示.
某城市要建宜居的新城,准备引进优秀企业进行城市建设.这个城市的甲区、乙区分别对6个企业进行评估,综合得分情况如茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
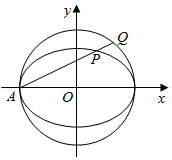 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com