练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．记f（n）=（3n+2）（C${\;}_{2}^{2}$+C${\;}_{3}^{2}$+C${\;}_{4}^{2}$+…+C${\;}_{n}^{2}$）（n≥2，n∈N*）．
    （1）求f（2），f（3），f（4）的值；
    （2）当n≥2，n∈N*时，试猜想所有f（n）的最大公约数，并证明．

    分析 （1）由组合数的性质可得f（n）=（3n+2）Cn+13，代值计算即可，
    （2）由（1）中结论可猜想所有f（n）的最大公约数为4．用数学归纳法证明所有的f（n）都能被4整除即可．

    解答 解：（1）因为f（n）=（3n+2）（C22+C32+C42+…+Cn2）=（3n+2）Cn+13，
    所以f（2）=8，f（3）=44，f（4）=140．
    （2）由（1）中结论可猜想所有f（n）的最大公约数为4．
    下面用数学归纳法证明所有的f（n）都能被4整除即可．
    （ⅰ）当n=2时，f（2）=8能被4整除，结论成立；                  
    （ⅱ）假设n=k时，结论成立，即f（k）=（3k+2）Ck+13能被4整除，
    则当n=k+1时，f（k+1）=（3k+5）Ck+23=（3k+2）Ck+13+3Ck+23=（3k+2）（Ck+13+Ck+12）+（k+2）Ck+12，
    =（3k+2）Ck+13+（3k+2）Ck+12+（k+2）Ck+12，
    =（3k+2）Ck+13+4（k+1）Ck+12，
    此式也能被4整除，即n=k+1时结论也成立．
    综上所述，所有f（n）的最大公约数为4．

    点评 本题考查数学归纳法，考查推理证明的能力，假设n=k（k∈N*）时命题成立，去证明则当n=k+1时，用上归纳假设是关键，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=|2x-1|．
    （1）若不等式f（x+$\frac{1}{2}$）≤2m+1（m＞0）的解集为[-2，2]，求实数m的值；
    （2）对任意x，y∈R，求证：f（x）≤2y+$\frac{4}{{2}^{y}}$+|2x+3|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{2\sqrt{5}}}{5}$，直线mx+y+1=1恒过椭圆的一个顶点．
    （I）求椭圆的标准方程；
    （Ⅱ）设O为坐标原点，P为椭圆的右焦点，过F的直线l（l不与坐标轴垂直）交椭圆于A，B两点，C为AB的中点，D为A关于x轴的对称点．
    （i）求证：直线OC与过点F且与l垂直的直线的交点在直线x=$\frac{5}{2}$上；
    （ii）在x轴上是否存在定点T，使B、D、T三点共线？若存在，求出T点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=x+alnx（a∈R）．
    （1）若曲线y=f（x）在点（1，f（1））处与直线y=3x-2相切，求a的值；
    （2）函数g（x）=f（x）-kx2有两个零点x1，x2，试判断$g'（{\frac{{{x_1}+{x_2}}}{2}}）$的符号，并证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

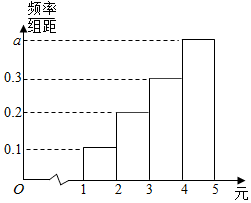    5．甲、乙、丙三人参加微信群抢红包游戏，规则如下：每轮游戏发10个红包，每个红包金额在[1，5]产生．已知在每轮游戏中所产生的10个红包金额的频率分布直方图如图所示．
    （Ⅰ）求a的值，并根据频率分布直方图，估计10个红包金额的中位数；
    （Ⅱ）以频率分布直方图中的频率作为概率，若甲抢到来自[2，4）中3个红包，求其中一个红包来自[2，3），另2个红包来自[3，4）的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

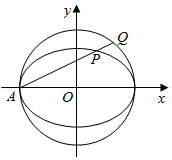    15．如图，在平面直角坐标系xOy中，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，长轴长为4，过椭圆的左顶点A作直线l，分别交椭圆和圆x2+y2=a2于相异两点P，Q．
    （1）若直线l的斜率为$\frac{1}{2}$，求$\frac{AP}{AQ}$的值；
    （2）若$\overrightarrow{PQ}$=λ$\overrightarrow{AP}$，求实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．如图，在五面体ABCDE中，AD⊥平面ABC，AD∥BE∥CF，△ABC为等边三角形，AB=2$\sqrt{3}$，BE=2，AD=3，CF=4，M为EF的中点．
    （Ⅰ）求证：DM∥平面ABC；
    （Ⅱ）求直线CD与平面DEF所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知非零向量$\overrightarrow{AB}$，$\overrightarrow{AC}$满足（$\frac{\overrightarrow{AB}}{|AB|}$+$\frac{\overrightarrow{AC}}{|AC|}$）•$\overrightarrow{BC}$=0，且$\frac{\overrightarrow{AB}}{|AB|}$•$\frac{\overrightarrow{AC}}{|AC|}$=$\frac{1}{2}$，则△ABC的形状是（　　）
    A．三边均不相等的三角形B．直角三角形
    C．等腰（非等边）三角形D．等边三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．数列{an}的前n项和为Sn，若a2=4，且Sn=an+1-2．
    （Ⅰ）求数列{an}的通项公式：
    （Ⅱ）若cn=-20+log2a4n，求{cn}的前n项和Tn的最小值．

    查看答案和解析>>

    同步练习册答案