Question

13．已知点A（-1，1）及圆C：（x-3）²+（y-4）²=1，求过A的圆C的两切线的切点连线所在直线的方程．

Answer 1

分析 由题意求出以A，C为直径的圆的方程，化为一般式，再把已知圆的方程化为一般式，两圆方程作差可得过A的圆C的两切线的切点连线所在直线的方程．

解答 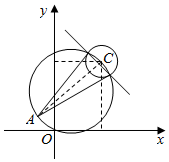解：如图，
由圆C：（x-3）²+（y-4）²=1，得圆心C（3，4），圆的半径为1，
又A（-1，1），则AC中点坐标为（1，$\frac{5}{2}$），
又|AC|=$\sqrt{（3+1）^{2}+（4-1）^{2}}=5$，
∴以AC为直径的圆的方程为：$（x-1）^{2}+（y-\frac{5}{2}）^{2}=\frac{25}{4}$，
整理得：x²+y²-2x-5y+1=0．①
化圆C：（x-3）²+（y-4）²=1为x²+y²-6x-8y+24=0．②
①-②得过A的圆C的两切线的切点连线所在直线的方程为4x+3y-23=0．

点评 本题考查圆的切线方程，训练了圆系方程的运用，体现了数学转化思想方法，是中档题．