
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
分析 由离散随机变量X的概率分布列的性质,结合等比数列性质和极限知识能求出常数a的值.
解答 解:∵离散随机变量X的概率函数为P(X=k)=$\frac{5a}{{2}^{k}}$,k=1,2,…,
∴$\underset{lim}{k→∞}$[5a($\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{k}}$)]=5a$\underset{lim}{k→∞}\frac{\frac{1}{2}[1-(\frac{1}{2})^{k}]}{1-\frac{1}{2}}$=5a=1,
∴常数a=$\frac{1}{5}$.
故选:C.
点评 本题考查常数值的求法,是基础题,解题时要认真审题,注意离散型随机变量、等比数列,极限知识的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
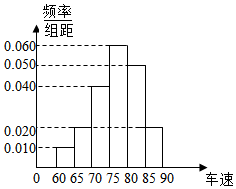 2016年“五一”期间,高速公路某服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽查一辆进行询问调查.共询问调查40名驾驶员.将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),
2016年“五一”期间,高速公路某服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽查一辆进行询问调查.共询问调查40名驾驶员.将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “f(0)=0”是“函数f(x)是奇函数”的必要不充分条件 | |
| B. | 若p:?x0∈R,x${\;}_{0}^{2}$-x0-1>0,则¬p:?x∈R,x2-x-1<0 | |
| C. | 命题“若x2-1=0,则x=1或x=-1”的否命题是“若x2-1≠0,则x≠1或x≠-1” | |
| D. | 命题p和命题q有且仅有一个为真命题的充要条件是(¬p∧q)∨(¬q∧p)为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 14 | C. | 10 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com