
分析 由题意得X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的数学期望.
解答 解:老师把4本不同的数学参考书和2本不同的英语参考书发给甲、乙两位同学,每人3本,
基本事件总数n=$\frac{{C}_{6}^{3}{C}_{3}^{3}}{{A}_{2}^{2}}•{A}_{2}^{2}$=20,
由题意得X的可能取值为0,1,2,
P(X=0)=$\frac{{C}_{4}^{3}}{20}$=$\frac{1}{5}$,
P(X=1)=$\frac{{C}_{2}^{1}{C}_{4}^{2}}{20}$=$\frac{3}{5}$,
P(X=2)=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{20}$=$\frac{1}{5}$,
∴X的数学期望为EX=$0×\frac{1}{5}+1×\frac{3}{5}+2×\frac{1}{5}$=1.
故答案为:1.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意排列组合知识的合理运用.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x | B. | y=x+1 | C. | y=1 | D. | y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
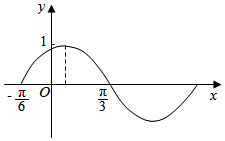 函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<$\frac{π}{2}}$) 的部分图象 如图所示,其最小正周期为π;如果x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{{\sqrt{3}}}{2}$.
函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<$\frac{π}{2}}$) 的部分图象 如图所示,其最小正周期为π;如果x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com