
分析 (1)由已知条件利用对立事件概率计算公式能求出单个坑不需要补种的概率.
(2)用ξ表示需要补种的坑数,则ξ~B(3,0.875),由此能求出ξ的分布列.
(3)由题意知一共种了3个坑,每个坑至多补种一次,每补种1个坑需10元,得到变量X的可能取值是0,10,20,30,分别求出相应的概率,由此能求出变量X的分布列,从而能求出X的期望与方差.
解答 解:(1)∵9粒种子分种在3个坑中,每坑3粒,每粒种子发芽的概率为0.5.
若一个坑内至少有1粒种子发芽,则这个坑内不需要补种,
若一个坑内的种子都没发芽,则这个坑需要补种,
∴单个坑不需要补种的概率p=1-0.53=0.875.
(2)用ξ表示需要补种的坑数,则ξ~B(3,0.875),
P(ξ=0)=C330.8753=0.670,
P(ξ=1)=C320.8752×0.125=0.287,
P(ξ=2)=C31×0.875×0.1252=0.041,
P(ξ=3)=0.1253=0.002,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | 0.670 | 0.287 | 0.041 | 0.002 |
| X | 0 | 10 | 20 | 30 |
| P | 0.670 | 0.287 | 0.041 | 0.002 |
点评 考查运用概率知识解决实际问题的能力,对立事件是指同一次试验中,不会同时发生的事件,遇到求用至少来表述的事件的概率时,往往先求它的对立事件的概率.


科目:高中数学 来源: 题型:解答题
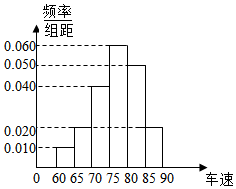 2016年“五一”期间,高速公路某服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽查一辆进行询问调查.共询问调查40名驾驶员.将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),
2016年“五一”期间,高速公路某服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽查一辆进行询问调查.共询问调查40名驾驶员.将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>4或x<0} | B. | {x|1<x<4} | C. | {x|1<x≤4} | D. | {x|1≤x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 14 | C. | 10 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂对某产品的产量与单位成本的资料分析后有如表数据:
某工厂对某产品的产量与单位成本的资料分析后有如表数据:| 月 份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量x千件 | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本y元/件 | 73 | 72 | 71 | 73 | 69 | 68 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com