
 某工厂对某产品的产量与单位成本的资料分析后有如表数据:
某工厂对某产品的产量与单位成本的资料分析后有如表数据:| 月 份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量x千件 | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本y元/件 | 73 | 72 | 71 | 73 | 69 | 68 |
分析 (1)根据所给的六组数据写出六个有序数对,在平面直角坐标系上点出对应的点,得到散点图,观察散点图呈带状分布,知产量与单位成本是线性相关.
(2)做出横标和纵标的平均数,得到这组数据的样本中心点,求出利用最小二乘法所需要的数据,代入关于b的公式,求出线性回归方程的系数,再求出a的值,得到方程.
解答 解:(1)根据所给的六组数据写出六个有序数对,在平面直角坐标系上点出对应的点,得到散点图,
观察散点图呈带状分布,知产量与单位成本是线性相关
(2)x1y1+x2y2+…+x6y6=1481,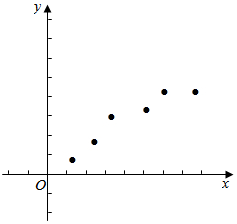
$\overline x=\frac{21}{6},\overline y=71,\sum_{i=1}^6{x_i^2}=79,\sum_{i=1}^6{{x_i}{y_i}}=1481$,
代入公式得:$\widehat{b}$=$\frac{1481-6×\frac{21}{6}×71}{79-6{×(\frac{21}{6})}^{2}}$≈-1.82,
$\widehat{a}$=71-(-1.82)×$\frac{21}{6}$≈77.37,
故线性回归方程为:$\hat{y}$=77.37-1.82x.
点评 本题考查线性回归方程的求解,本题解题的关键是正确求解线性回归方程的系数,这里的运算比较麻烦,容易出错.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{25}$ | B. | -$\frac{18}{25}$ | C. | -$\frac{12}{25}$ | D. | -$\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{1}{8}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | $\frac{2}{3}$π | x1 | $\frac{8}{3}$π | x2 | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p:?x>0,都有x2>0,则?p:?x0≤0,使得x02≤0 | |
| B. | 若命题p和p∨q都是真命题,则命题q也是真命题 | |
| C. | 在△ABC中,a,b,c是角A,B,C的对边,则a<b的充要条件是cosA>cosB | |
| D. | 命题“若x2+x-2=0,则x=-2或x=1”的逆否命题是“x≠-2或x≠1,则x2+x-2≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在正方体ABCD-A1B1C1D1中,棱长AB=2,M,N,P分别是C1C,BC1,C1D1的中点.
在正方体ABCD-A1B1C1D1中,棱长AB=2,M,N,P分别是C1C,BC1,C1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com