Question

7．在正方体ABCD-A₁B₁C₁D₁中，棱长AB=2，M，N，P分别是C₁C，BC₁，C₁D₁的中点．
（1）直线A₁C₁交PN于点E，直线AC₁交平面MNP于点F，求证：M，E，F三点共线．
（2）求三棱锥D-MNP的体积．

Answer 1

分析 （1）利用公理3证明ME为平面AA₁C₁C与平面PMN的交线，进一步证明F在两面的交线上得M，E，F三点共线．
（2）利用等积法把三棱锥D-MNP的体积转化为三棱锥N-DMP的条件求解．

解答 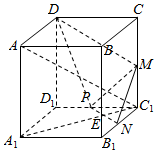证明：（1）∵A₁C₁∩PN=E，
∴E∈A₁C₁，E∈PN，则E∈平面AA₁C₁C，E∈平面MPN
又∵M∈CC₁，
∴M∈平面AA₁C₁C，
又M∈平面PMN，
∴平面AA₁C₁C∩平面PMN=ME，
∵AC₁∩平面MPN=F，
∴F∈平面PMN，F∈平面AA₁C₁C，
∴点F在直线ME上，则M，E，F三点共线．
解：（2）${V}_{D-MNP}={V}_{N-MDP}=\frac{1}{3}{S}_{△MDP}•N{C}_{1}$，
又${S}_{△MDP}=2×2-\frac{1}{2}×2×1-\frac{1}{2}×1×1-\frac{1}{2}×2×1=\frac{3}{2}$，
∴${V}_{D-MNP}=\frac{1}{3}×\frac{3}{2}×1=\frac{1}{2}$．

点评 本题考查平面的基本性质即推论，考查了利用等积法求三棱锥的体积，是中档题．