Question

19．已知正四棱锥底面正方形的边长为4，高与斜高的夹角为30°，求正四棱锥的侧面积、全面积、体积．

Answer 1

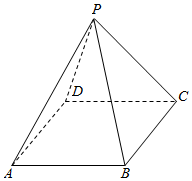
分析 利用已知中，正四棱锥底面正方形的边长为4cm，高与斜高的夹角为30°，求出正四棱锥的高PO，斜高PE，底面边心距OE组成直角△POE，求出斜高和高，代入棱锥的侧面积、表面积、体积公式，即可求得答案．

解答 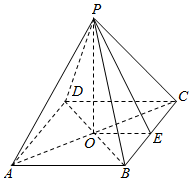解：（1）如图，正四棱锥的高PO，斜高PE，底面边心距OE组成直角△POE．
∵OE=2cm，∠OPE=30°，
∴斜高h′=PE=$\frac{OE}{sin30°}$=4（cm），
∴S_正棱锥侧=$\frac{1}{2}$Ch′=$\frac{1}{2}$×4×4×4=32（cm²），
（2）S_正棱锥全=4²+32=48（cm²）． 
（3）V=$\frac{1}{3}×4×4×\sqrt{16-4}$=$\frac{32\sqrt{3}}{3}$．

点评 本题考查的知识点是棱锥的体积，主要通过正棱锥的高、斜高、底面边心距组成的直角三角形寻找到各量的关系，并求解．