
 如图,在边长为10(单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它的四个角沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.问正四棱锥的体积V(x)何时最大?最大值是多少?
如图,在边长为10(单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它的四个角沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.问正四棱锥的体积V(x)何时最大?最大值是多少? 分析 用x表示出四棱锥的侧棱长和对角线长,计算出棱锥的高,得到V(x)的解析式,利用导数与极值的关系求出最大体积.
解答 解:棱锥的侧棱长为l=$\sqrt{{5}^{2}+{x}^{2}}$=$\sqrt{25+{x}^{2}}$,棱锥的底面对角线长为10-2x,显然0<x<5.
∴棱锥的高h=$\sqrt{{l}^{2}-(5-x)^{2}}$=$\sqrt{10x}$,棱锥的底面边长为$\frac{10-2x}{\sqrt{2}}$=$\sqrt{2}$(5-x).
∴棱锥的体积V(x)=$\frac{1}{3}$×($\sqrt{2}$(5-x))2×$\sqrt{10x}$=$\frac{2\sqrt{10}}{3}(5-x)^{2}\sqrt{x}$.
∴V′(x)=$\frac{2\sqrt{10}}{3}$•[2(x-5)$\sqrt{x}$+(x-5)2•$\frac{\sqrt{x}}{2x}$]=$\frac{2\sqrt{10}}{3}$•(x-5)•$\sqrt{x}$•$\frac{5x-5}{2x}$.
令V′(x)=0,得x=1,
当0<x<1时,V′(x)>0,当1<x<5时,V′(x)<0.
∴当x=1时,V(x)取得最大值,最大值为V(1)=$\frac{32\sqrt{10}}{3}$.
点评 本题以折叠图形为依托,考查空间几何体的体积的求法,通过函数的对数求法函数的值的方法,考查空间想象能力与计算能力;解题中注意函数的定义域,导数的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
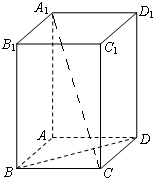 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com