

分析 (1)取AE中点O,连结OB,OD′,则OD′⊥AE,根据面面垂直的性质得出OD′⊥平面ABCE,故而∠D′BO为直线D′B与平面ABCE所成的角,计算OD′和OB,则tan∠D′BO=$\frac{D′O}{OB}$.
(2)OD′为四棱锥D′-ABCE的高,底面为直角梯形,代入体积公式计算即可;
(3)过F分别作AD′,BC的平行线FG,FE,则∠EFG为异面直线AD′与BC所成的角,利用勾股定理的逆定理证明AD′⊥BD′,结合AD′⊥D′E,AD′∥FG得出FG⊥平面BD′E,于是FG⊥EG,计算出FG,EF,利用三角函数定义计算cos∠GFE,得出∠EFG的大小.
解答 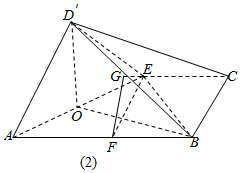 解;(1)取AE中点O,连结OB,OD′,
解;(1)取AE中点O,连结OB,OD′,
∵D′A=D′E,O是AE的中点,∴D′O⊥AE
∵D′-AE-B是直二面角,∴平面D′AE⊥平面ABCE.
又平面D′AE∩平面ABCE=AE,D′O?平面D′AE,
∴D′O⊥平面ABCE,
∴∠D′BO是直线D′B与平面ABCE所成的角.
∵D′A=D′E=a,D′O⊥AE,∠AD′E=90°,
∴AE=$\sqrt{2}a$,AO=D′O=$\frac{1}{2}AE$=$\frac{\sqrt{2}}{2}$a,∠D′AE=∠BAO=45°.
∴在△AOB中,由余弦定理得OB=$\sqrt{O{A}^{2}+A{B}^{2}-2OA•AB•cos45°}$=$\frac{\sqrt{10}}{2}$a.
∴tan∠D′BO=$\frac{D′O}{OB}$=$\frac{\frac{\sqrt{2}a}{2}}{\frac{\sqrt{10}a}{2}}$=$\frac{\sqrt{5}}{5}$.
(2)∵四边形ABCE是直角梯形,
∴SABCE=$\frac{1}{2}$(a+2a)•a=$\frac{3}{2}$a2.
又∵D′O 是四棱锥的高且D′O=$\frac{\sqrt{2}}{2}$a,
∴VD′-ABCE=$\frac{1}{3}$×$\frac{3}{2}$a2×$\frac{\sqrt{2}}{2}$a=$\frac{\sqrt{2}}{4}$a3.
(3)取AB的中点F,和D′B的中点G,并连结EF、EG、FG,
则EF∥BC,FG∥AD′,
∴∠GFE就是异面直线AD′与BC所成的角.
∵D′B=$\sqrt{D′{O}^{2}+O{B}^{2}}$=$\sqrt{3}$a,AD′=a,AB=2a,
∴AD′2+BD′2=AB2,∴AD′⊥BD′,
又AD′⊥D′E,BD′?平面BD′E,D′E?平面BD′E,BD′∩D′E=D′,
∴AD′⊥平面BD′E,
∴FG⊥平面BD′E,∵EG?平面BD′E,
∴FG⊥GE,即△EFG是直角三角形.
∵EF=BC=a,FG=$\frac{1}{2}$AD′=$\frac{1}{2}$a,
∴cos∠GFE=$\frac{FG}{EF}$=$\frac{1}{2}$,
∴异面直线AD′与BC所成的角为60°.
点评 本题考查了线面垂直的判定,空间角的作法与计算,棱锥的体积计算,属于中档题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 10 | C. | 9 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | $\frac{2}{3}$π | x1 | $\frac{8}{3}$π | x2 | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在正方体ABCD-A1B1C1D1中,棱长AB=2,M,N,P分别是C1C,BC1,C1D1的中点.
在正方体ABCD-A1B1C1D1中,棱长AB=2,M,N,P分别是C1C,BC1,C1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
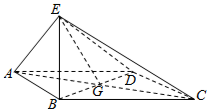 如图四边形ABCD为菱形,G为AC与BD交点,BE⊥平面ABCD,
如图四边形ABCD为菱形,G为AC与BD交点,BE⊥平面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在边长为10(单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它的四个角沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.问正四棱锥的体积V(x)何时最大?最大值是多少?
如图,在边长为10(单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它的四个角沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.问正四棱锥的体积V(x)何时最大?最大值是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com