
分析 (1)设直线l:x=ty+m,代入抛物线y2=4x,利用韦达定理及向量数量积公式即可得到结论.
(2)根据弦长公式得到t=±1,再分别求出相对应的△AOB的外接圆的方程.
解答 解:(1)直线l过定点(4,0).证明如下:
设直线l的方程为x=ty+m,A(x1,y1),B(x2,y2),则OA⊥OB?x1x2+y1y2=0
即$({1+{t^2}}){y_1}{y_2}+mt({{y_1}+{y_2}})+{m^2}=0$ ①
由$\left\{\begin{array}{l}{y^2}=4x\\ x=ty+m\end{array}\right.∴{y^2}-4ty-4m=0$,
∴y1+y2=4t,y1y2=-4m ②
由 ①②得m2-4m=0,
∴m=4
故直线l过定点(4,0).
(2)由(1)知$|{AB}|=\sqrt{({1+{t^2}})[{{{({{y_1}+{y_2}})}^2}-4{y_1}{y_2}}]}=4\sqrt{({1+{t^2}})({{t^2}+4})}=4\sqrt{10}$,
∴t2=1,
①若t=1,则y1+y2=4,x1+x2=12,∴外接圆方程为(x-6)2+(y-2)2=40
②若t=-1,则y1+y2=-4,x1+x2=4,∴外接圆方程为(x-2)2+(y+2)2=8
故外接圆方程为(x-6)2+(y-2)2=40或(x-2)2+(y+2)2=8.
点评 本题考查直线与抛物线的位置关系,考查向量知识的运用,正确运用韦达定理是关键,解题时要注意弦长公式的合理运用,考查圆的方程,考查学生分析解决问题的能力,属于中档题


科目:高中数学 来源: 题型:解答题
| x | $\frac{2}{3}$π | x1 | $\frac{8}{3}$π | x2 | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在边长为10(单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它的四个角沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.问正四棱锥的体积V(x)何时最大?最大值是多少?
如图,在边长为10(单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它的四个角沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.问正四棱锥的体积V(x)何时最大?最大值是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}-2$ | B. | $\frac{3\sqrt{2}}{2}$-1 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{2}$+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知直线l与抛物线y2=2x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-4,
如图,已知直线l与抛物线y2=2x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-4,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
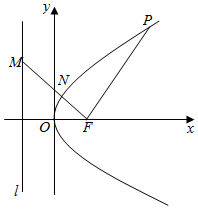 如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )
如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com