
分析 (1)先求出基本事件总数n=${C}_{4}^{2}{C}_{2}^{1}$,A和B不都去参加的对立事件是A和B都去参加,由此利用对立事件概率计算公式能求出A和B不都去参加的概率.
(2)由已知得X的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(1)∵某小组有A、B、C、D、E、F六位同学,其中A、B、C、D四位同学成绩较好,E、F两位同学成绩较弱.
某次活动上,决定由两位成绩较好的同学和一位成绩较差的同学组队参加,
基本事件总数n=${C}_{4}^{2}{C}_{2}^{1}$=12,
A和B不都去参加的对立事件是A和B都去参加,
∴A和B不都去参加的概率P=1-$\frac{{C}_{2}^{2}{C}_{2}^{1}}{{C}_{4}^{2}{C}_{2}^{1}}$=1-$\frac{2}{12}$=$\frac{5}{6}$.
(2)由已知得X的可能取值为1,2,3,4,
P(X=1)=$\frac{2}{6}$=$\frac{1}{3}$,
P(X=2)=$\frac{4}{6}×\frac{2}{5}$=$\frac{4}{15}$,
P(X=3)=$\frac{4}{6}×\frac{3}{5}×\frac{2}{4}$=$\frac{1}{5}$,
P(X=4)=$\frac{4}{6}×\frac{3}{5}×\frac{2}{4}×\frac{2}{3}$=$\frac{2}{15}$,
P(X=5)=$\frac{4}{6}×\frac{3}{5}×\frac{2}{4}×\frac{1}{3}×\frac{2}{2}$=$\frac{1}{15}$,
∴X的分布列为:
| X | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{3}$ | $\frac{4}{15}$ | $\frac{1}{5}$ | $\frac{2}{15}$ | $\frac{1}{15}$ |
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意对立事件概率计算公式和相互独立事件概率乘法公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | y=x | B. | y=x+1 | C. | y=1 | D. | y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
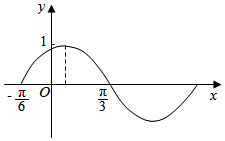 函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<$\frac{π}{2}}$) 的部分图象 如图所示,其最小正周期为π;如果x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{{\sqrt{3}}}{2}$.
函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<$\frac{π}{2}}$) 的部分图象 如图所示,其最小正周期为π;如果x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 10 | C. | 9 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{25}$ | B. | -$\frac{18}{25}$ | C. | -$\frac{12}{25}$ | D. | -$\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | $\frac{2}{3}$π | x1 | $\frac{8}{3}$π | x2 | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在边长为10(单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它的四个角沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.问正四棱锥的体积V(x)何时最大?最大值是多少?
如图,在边长为10(单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它的四个角沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.问正四棱锥的体积V(x)何时最大?最大值是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com