
分析 方法一、运用作差比较法,因式分解即可得证;
方法二、运用不等式的性质:可加性,即可得证.
解答 证法一:由x>y>0,可得x-y>0,
x+$\frac{1}{y}$-(y+$\frac{1}{x}$)=(x-y)+($\frac{1}{y}$-$\frac{1}{x}$)
=(x-y)+$\frac{x-y}{xy}$=(x-y)(1+$\frac{1}{xy}$)>0,
则x+$\frac{1}{y}$>y+$\frac{1}{x}$.
证法二、由x>y>0,可得$\frac{1}{x}$<$\frac{1}{y}$,
即为$\frac{1}{y}$>$\frac{1}{x}$>0,
由不等式的可加性可得x+$\frac{1}{y}$>y+$\frac{1}{x}$.
点评 本题考查不等式的证明,注意运用作差法和不等式的性质:可加性,考查运算和推理能力,属于基础题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,在边长为10(单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它的四个角沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.问正四棱锥的体积V(x)何时最大?最大值是多少?
如图,在边长为10(单位:m)的正方形铁皮的四周切去四个全等的等腰三角形,再把它的四个角沿着虚线折起,做成一个正四棱锥的模型.设切去的等腰三角形的高为x m.问正四棱锥的体积V(x)何时最大?最大值是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知直线l与抛物线y2=2x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-4,
如图,已知直线l与抛物线y2=2x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-4,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
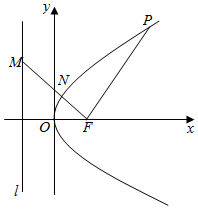 如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )
如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5\sqrt{2}}{6}$ | B. | 3$\sqrt{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com