
分析 (1)设设A(x1,y1),B(x2,y2),M(x0,y0),求切线MA,切线MB的方程,可得2x0=x1+x2,y0=x1x2,设直线AB的方程是y=kx+b,代入y=x2得x0=$\frac{1}{2}$k,y0=-b,代入y0=x0-1得-b=$\frac{1}{2}$k-1,即可证明结论;
(2)由两点间距离公式可求|AB|,由点到直线的距离公式可求点M到直线AB的距离d,由三角形面积公式及二次函数的性质即可得解.
解答 (1)证明:设A(x1,y1),B(x2,y2),M(x0,y0).
∵y=x2,∴y′=2x.
于是在点A处的切线方程为y-y1=2x1(x-x1),化为y=2x1x-x12.①
同理在点B处的切线方程为y=2x2x-x22.②
由①②得2x0=x1+x2,y0=x1x2,显然直线AB存在斜率.
设直线AB的方程是y=kx+b,代入y=x2得x2-kx-b=0,
∴x1+x2=k,x1x2=-b,即x0=$\frac{1}{2}$k,y0=-b,
代入y0=x0-1得-b=$\frac{1}{2}$k-1
∴y=kx-$\frac{1}{2}$k+1
∴y-1=k(x-$\frac{1}{2}$)
令x-$\frac{1}{2}$=0,可得y-1=0,∴x=$\frac{1}{2}$,y=1.
因此直线AB恒过定点($\frac{1}{2}$,1);
(2)解:由(1)得|AB|=$\sqrt{1+{k}^{2}}•\sqrt{{k}^{2}+4b}$=$\sqrt{1+{k}^{2}}•\sqrt{{k}^{2}-2k+4}$
点M到直线AB的距离是d=$\frac{\frac{1}{2}({k}^{2}-2k+4)}{\sqrt{1+{k}^{2}}}$
△MAB的面积=$\frac{1}{2}$|AB|•d=$\frac{1}{4}({k}^{2}-2k+4)^{\frac{3}{2}}$≥$\frac{3\sqrt{3}}{4}$,
当k=1时△MAB的面积取得最小值$\frac{3\sqrt{3}}{4}$,M的坐标为($\frac{1}{2}$,-$\frac{1}{2}$).
点评 本题主要考查了直线与圆锥曲线的关系,两点间距离公式,点到直线距离公式,直线的方程等知识的应用,难度大.熟练掌握导数的几何意义及其切线方程是解题的关键.


科目:高中数学 来源: 题型:解答题
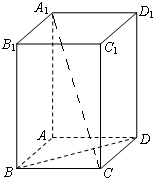 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com