
分析 (Ⅰ)由题意可得c=2,求得焦点坐标,运用椭圆的定义可得2a=4$\sqrt{2}$,即a=2$\sqrt{2}$,运用a,b,c的关系,可得b,进而得到椭圆方程;
(Ⅱ)根据椭圆的对称性,直线AB与x轴不垂直,设直线AB:y=kx+m,代入椭圆方程,运用韦达定理和弦长公式,求得O到直线AB的距离,依题意,|AM|=|BM|,运用两点的距离公式,化简可得k,m的等式,讨论k=0,k≠0,运用基本不等式和二次函数的最值求法,即可得到所求面积的最大值.
解答 解:(Ⅰ)依题意,2c=4,椭圆Σ的焦点为F1(-2,0),F2(2,0),
由椭圆的定义可得2a=|PF1|+|PF2|=$\sqrt{(2+2)^{2}+(\sqrt{2})^{2}}$+$\sqrt{(2-2)^{2}+(\sqrt{2})^{2}}$
=3$\sqrt{2}$+$\sqrt{2}$=4$\sqrt{2}$,
即有a=2$\sqrt{2}$,则b2=a2-c2=4,
则椭圆Σ的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(Ⅱ)根据椭圆的对称性,直线AB与x轴不垂直,设直线AB:y=kx+m,
由$\left\{\begin{array}{l}\frac{x^2}{8}+\frac{y^2}{4}=1\\ y=kx+m\end{array}\right.$得,(2k2+1)x2+4kmx+2m2-8=0,
设A(x1,y1),B(x2,y2),
则${x_1}+{x_2}=-\frac{4km}{{2{k^2}+1}}$,${x_1}•{x_2}=\frac{{2{m^2}-8}}{{2{k^2}+1}}$,
$|AB|=\sqrt{{k^2}+1}|{x_1}-{x_2}|=\frac{{2\sqrt{{k^2}+1}\sqrt{16{k^2}+8-2{m^2}}}}{{2{k^2}+1}}$,
O到直线AB的距离$d=\frac{|m|}{{\sqrt{1+{k^2}}}}$,
△OAB的面积$S=\frac{1}{2}×|AB|×d=\frac{{\sqrt{2{m^2}(8{k^2}+4-{m^2})}}}{{2{k^2}+1}}$,
依题意,|AM|=|BM|,即${x_1}^2+{({y_1}-1)^2}={x_2}^2+{({y_2}-1)^2}$,
即有(x1-x2)(x1+x2)+(y1-y2)(y1+y2-2)=0,
$({x_1}+{x_2})+\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}[k({x_1}+{x_2})+2m-2]=0$,
即为(k2+1)(x1+x2)+k(2m-2)=0,代入整理得,k(2k2+m+1)=0,
若k=0,则$S=\sqrt{2{m^2}(4-{m^2})}≤2\sqrt{2}$,等号当且仅当$m=-\sqrt{2}$时成立;
若k≠0,则2k2+m+1=0,$S=\sqrt{2(-4m-{m^2})}≤2\sqrt{2}$,
等号当且仅当m=-2,$k=±\frac{{\sqrt{2}}}{2}$时成立.
综上所述,△OAB面积的最大值为$2\sqrt{2}$.
点评 本题考查椭圆的方程的求法,注意运用椭圆的定义,考查三角形的面积的最值的求法,注意联立直线方程与椭圆方程,运用韦达定理和弦长公式,以及点到直线的距离公式,同时考查基本不等式和二次函数的最值求法,以及化简运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}-2$ | B. | $\frac{3\sqrt{2}}{2}$-1 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{2}$+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
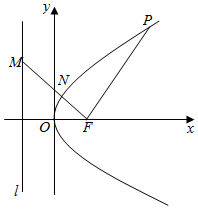 如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )
如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增加了$\frac{1}{2k+1}$这一项 | |
| B. | 增加了$\frac{1}{2k+1}$和$\frac{1}{2k+2}$两项 | |
| C. | 增加了$\frac{1}{2k+1}$和$\frac{1}{2k+2}$两项,同时减少了$\frac{1}{k}$这一项 | |
| D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
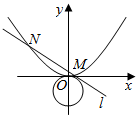 过抛物线L:x2=2py(p>0)的焦点F且斜率为$\frac{3}{4}$的直线与抛物线L在第一象限的交点为P,且|PF|=5.
过抛物线L:x2=2py(p>0)的焦点F且斜率为$\frac{3}{4}$的直线与抛物线L在第一象限的交点为P,且|PF|=5.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com