
分析 (Ⅰ)由余弦定理,正弦定理化简已知可得:7(a2+b2)=5c2,c2=$\frac{7}{2}$ab,从而利用余弦定理可求cosC=-$\frac{1}{2}$,结合范围C∈(0,π)即可求得∠C的值.
(Ⅱ)利用三角形面积公式可求ab=2,由(Ⅰ)知,c2=7,a2+b2=5,联立可求a,b的值,利用正弦定理即可求得sinA的值.
解答 解:(Ⅰ)由题意及余弦定理得,a2+b2+5ab$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=0,
即7(a2+b2)=5c2,---------------------------------------------------(2分)
由题意及正弦定理得,c2=$\frac{7}{2}$ab,-------------------------------------(4分)
故cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{-\frac{2{c}^{2}}{7}}{2ab}$=-$\frac{1}{2}$,--------------------(6分)
因为C∈(0,π),∠C=$\frac{2π}{3}$,--------------------------------------(7分)
(Ⅱ)因为S△ABC=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{2}$,即ab=2 ①.--------------------------(9分)
由(Ⅰ)知,c2=7,a2+b2=5 ②.------------------------------------(11分)
联立①②得$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$,或$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$.-----------------------------------------------(13分)
由正弦定理$\frac{a}{sinA}=\frac{c}{sinC}$得,sinA=$\frac{\sqrt{21}}{14}$或sinA=$\frac{\sqrt{21}}{7}$.-------(15分)
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{31}{16}$ | B. | $\frac{15}{16}$ | C. | $\frac{15}{8}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
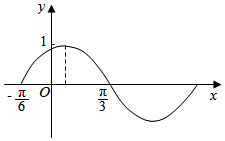 函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<$\frac{π}{2}}$) 的部分图象 如图所示,其最小正周期为π;如果x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{{\sqrt{3}}}{2}$.
函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<$\frac{π}{2}}$) 的部分图象 如图所示,其最小正周期为π;如果x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{25}$ | B. | -$\frac{18}{25}$ | C. | -$\frac{12}{25}$ | D. | -$\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p:?x>0,都有x2>0,则?p:?x0≤0,使得x02≤0 | |
| B. | 若命题p和p∨q都是真命题,则命题q也是真命题 | |
| C. | 在△ABC中,a,b,c是角A,B,C的对边,则a<b的充要条件是cosA>cosB | |
| D. | 命题“若x2+x-2=0,则x=-2或x=1”的逆否命题是“x≠-2或x≠1,则x2+x-2≠0” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com