
分析 (1)运用“相似椭圆”的定义,讨论s>2,0<s<2,列出等式,解方程可得s;
(2)求得A,D的坐标,可得直线l1与直线l2的方程,代入椭圆G的方程,运用判别式为0,求得|k1|,|k2|,再由基本不等式即可得到所求最小值;
(3)求得椭圆H的方程,设出椭圆H上的任意一点C(x0,y0),代入椭圆H的方程;设△ABC的垂心M的坐标为(xM,yM),运用垂心的定义,结合两直线垂直的条件:斜率之积为-1,化简整理,可得M的坐标,代入椭圆E的方程即可得证.
解答 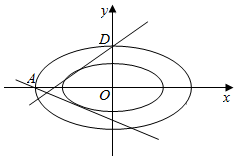 解:(1)显然椭圆E的方程为$\frac{x^2}{2}+{y^2}$=1,
解:(1)显然椭圆E的方程为$\frac{x^2}{2}+{y^2}$=1,
由椭圆E与F相似易得:
当s>2时$\frac{2}{s}=\frac{1}{2}$⇒s=4;
当0<s<2时$\frac{2}{2}=\frac{1}{s}$⇒s=1.
则s=4或1;
(2)易得$A(-\sqrt{2},0),D(0,1)$,
可得l1、l2的方程分别为$y={k_1}(x+\sqrt{2})$、y=k2x+1,
依题意联立:$\left\{{\begin{array}{l}{y={k_1}(x+\sqrt{2})}\\{\frac{x^2}{2}+{y^2}=λ}\end{array}}$⇒(1+2k12)x2+4$\sqrt{2}$k12x+4k12-2λ=0,
又直线l1与椭圆G相切,则△1=0(又0<λ<1),即32k14-4(1+2k12)(4k12-2λ)=0,
即|k1|=$\frac{1}{{\sqrt{2}}}\sqrt{\frac{λ}{1-λ}}$,
依题意再联立:$\left\{{\begin{array}{l}{y={k_2}x+1}\\{\frac{x^2}{2}+{y^2}=λ}\end{array}}$⇒(1+2k22)x2+4k2x+2-2λ=0,
又直线l2与椭圆G相切则△2=0(又0<λ<1),即16k22-4(1+2k22)(2-2λ)=0,
即|k2|=$\frac{1}{{\sqrt{2}}}\sqrt{\frac{1-λ}{λ}}$,
故|k1k2|=$\frac{1}{2}$,
即|k1|+|k2|≥2$\sqrt{|{k_1}{k_2}|}=\sqrt{2}$,当且仅当|k1|=|k2|时取到等号,此时λ=$\frac{1}{2}$,
所以当λ=$\frac{1}{2}$时|k1|+|k2|取得最小值$\sqrt{2}$;
(3)证明:显然椭圆E:$\frac{x^2}{2}+{y^2}$=1,由$\frac{t}{2}$=$\frac{2}{1}$,可得t=4,
即有椭圆H:$\frac{x^2}{2}+\frac{y^2}{4}$=1.
由椭圆H上的任意一点C(x0,y0),于是$\frac{{{x_0}^2}}{2}+\frac{{{y_0}^2}}{4}$=1①
设△ABC的垂心M的坐标为(xM,yM),
由CM⊥AB得xM=x0,
又AM⊥BC⇒$\frac{y_M}{{{x_M}+\sqrt{2}}}•\frac{y_0}{{{x_0}-\sqrt{2}}}$=-1,
将xM=x0代入$\frac{y_M}{{{x_M}+\sqrt{2}}}•\frac{y_0}{{{x_0}-\sqrt{2}}}$=-1,得x02=2-y0yM②
由①②得y0=2yM.
又x0=xM代入(1)得$\frac{{{x_M}^2}}{2}+{y_M}$2=1,
即△ABC的垂心M在椭圆E上.
点评 本题考查新定义的理解和运用,考查直线方程和椭圆方程联立,运用判别式为0,同时考查基本不等式的运用和三角形的垂心的判断,考查运算化简能力,属于中档题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某公司做了用户对其某产品满意度的问卷调查.随机抽取了20名用户(其中有7名男性用户和13名女性用户)的评分,得到如图所示茎叶图.对不低于75的评分,认为用户对产品满意,否则,认为不满意.已知对产品满意用户中男性有4名.
某公司做了用户对其某产品满意度的问卷调查.随机抽取了20名用户(其中有7名男性用户和13名女性用户)的评分,得到如图所示茎叶图.对不低于75的评分,认为用户对产品满意,否则,认为不满意.已知对产品满意用户中男性有4名.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{17}-1}}{4}$ | D. | 2$\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x | B. | y=x+1 | C. | y=1 | D. | y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
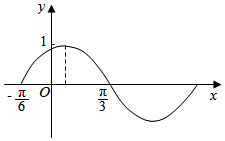 函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<$\frac{π}{2}}$) 的部分图象 如图所示,其最小正周期为π;如果x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{{\sqrt{3}}}{2}$.
函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<$\frac{π}{2}}$) 的部分图象 如图所示,其最小正周期为π;如果x1,x2∈(-$\frac{π}{6}$,$\frac{π}{3}}$),且f(x1)=f(x2),则f(x1+x2)=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com