
| A. | [-2,2] | B. | [-10,10] | C. | (-∞,-10]∪[10,+∞) | D. | (-∞,-2]∪[2,+∞) |
分析 先求出圆心和半径,比较半径和2$\sqrt{2}$,要求 圆上至少有三个不同的点到直线l:x-y+b=0的距离为2$\sqrt{2}$,则圆心到直线的距离应小于等于$\sqrt{2}$,用圆心到直线的距离公式,可求得结果.
解答 解:圆x2+y2-4x-4y-10=0整理为(x-2)2+(y-2)2=18,
∴圆心坐标为(2,2),半径为3$\sqrt{2}$,
要求圆上至少有三个不同的点到直线l:x-y+b=0的距离为2$\sqrt{2}$,
则圆心到直线的距离d=$\frac{|b|}{\sqrt{2}}$≤$\sqrt{2}$,
∴-2≤b≤2,
∴b的取值范围是[-2,2],
故选A.
点评 本题考查直线和圆的位置关系,圆心到直线的距离等知识,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -9 | C. | -7 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
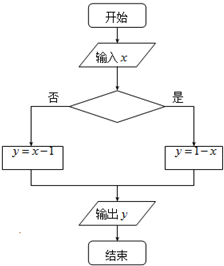 在如图所示的求函数f(x)=|x-1|的函数值的程序框图中,有六名学生在空白处的判断框内填入的条件分别是:①x≥1;②x>1;③x≤1;④x<1;⑤x≥0;⑥x≤0,其中正确的个数是( )
在如图所示的求函数f(x)=|x-1|的函数值的程序框图中,有六名学生在空白处的判断框内填入的条件分别是:①x≥1;②x>1;③x≤1;④x<1;⑤x≥0;⑥x≤0,其中正确的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
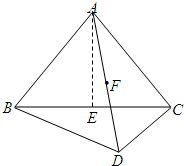 已知四面体ABCD中,AB=AC,BD=CD,平面ABC⊥平面BCD,E,F分别为棱BC和AD的中点.
已知四面体ABCD中,AB=AC,BD=CD,平面ABC⊥平面BCD,E,F分别为棱BC和AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{8}$ | B. | $-\frac{7}{8}$ | C. | $\frac{17}{25}$ | D. | $-\frac{17}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
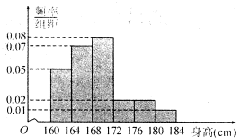 某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第一组[160,164],第二组[164,168],组方法得到的频率分布直方图.
某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第一组[160,164],第二组[164,168],组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com