Question

4．求（1）|x-3|+|x+1|的最小值；
（2）|x-3|-|x+1|的最大值．

Answer 1

分析 方法1：根据绝对值不等式进行求解即可．
方法2：根据绝对值的性质将绝对值表示成分段函数性质，利用数形结合进行求解．

解答 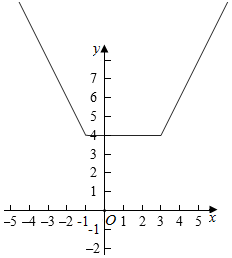解：（1）方法1：|x-3|+|x+1|≥|x-3-（x+1）|=|x-3-x-1|=4，
即|x-3|+|x+1|的最小值是4；
方法2：|x-3|+|x+1|=$\left\{\begin{array}{l}{-2x+2，}&{x＜-1}\\{4}&{-1≤x≤3}\\{2x-2，}&{x＞3}\end{array}\right.$，则对应的图象为，
则函数的最小值为4．
（2）方法1：|x-3|-|x+1|≤|x-3-x+-1|=4，
即|x-3|-|x+1|的最大值是4．
方法2：|x-3|-|x+1|=$\left\{\begin{array}{l}{4，}&{x＜-1}\\{-2x+2，}&{-1≤x≤3}\\{-4，}&{x≥3}\end{array}\right.$，
则对应的图象为：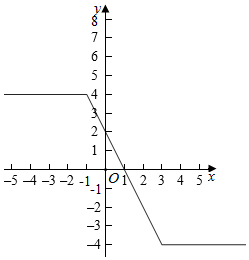

则函数的最大值为4．

点评 本题主要考查绝对值函数的最值的应用，一种方法是利用绝对值不等式的性质进行求解，另外一种是利用分段函数的图象和性质，考查学生的转化能力．