
【题目】如图所示,多面体ABCDEF中,已知平面ABCD是边长为3的正方形,![]() ,
,![]() ,EF到平面ABCD的距离为2,则该多面体的体积V为( )
,EF到平面ABCD的距离为2,则该多面体的体积V为( )
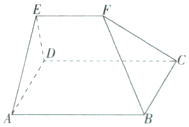
A.![]() B.5C.6D.
B.5C.6D.![]()
【答案】D
【解析】
方法一:连接EB,EC,AC,由等体法可得![]() ,再由
,再由![]() 以及棱锥的体积公式即可求解;方法二:设G,H分别为AB,DC的中点,连接EG,EH,GH,得三棱柱
以及棱锥的体积公式即可求解;方法二:设G,H分别为AB,DC的中点,连接EG,EH,GH,得三棱柱![]() ,则
,则![]() ,由
,由![]() 即可求解,方法三:延长EF至点M,使
即可求解,方法三:延长EF至点M,使![]() ,连接BM,CM,AF,DF,则多面体
,连接BM,CM,AF,DF,则多面体![]() 为斜三棱柱,由
为斜三棱柱,由![]() ,
,![]() 即可求解.
即可求解.
解法一:如图,连接EB,EC,AC,则![]() .
.
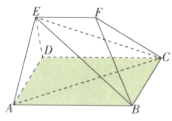
![]() ,
,![]()
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
解法二:如图,设G,H分别为AB,DC的中点,连接EG,EH,GH,
则![]() ,
,![]() ,
,![]() ,得三棱柱
,得三棱柱![]() ,
,

由题意得
![]()
![]() ,
,
![]() ,
,
![]() .
.
解法三:如图,延长EF至点M,使![]() ,连接BM,CM,AF,DF,
,连接BM,CM,AF,DF,
则多面体![]() 为斜三棱柱,其直截面面积
为斜三棱柱,其直截面面积![]() ,则
,则![]() .
.
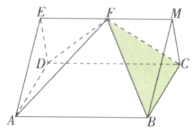
又![]() 平面BCM与平面ADE平行,F为EM的中点,
平面BCM与平面ADE平行,F为EM的中点,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,![]() .
.
故选:D


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,设倾斜角为
中,设倾斜角为![]() 的直线的参数方程为
的直线的参数方程为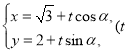 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立的极坐标系中,曲线
轴正半轴为极轴建立的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线与曲线
,直线与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)若![]() ,求直线的普通方程和曲线
,求直线的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为
为![]() 与
与![]() 的等比中项,其中
的等比中项,其中![]() ,求直线的斜率.
,求直线的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 满足
满足![]() .
.
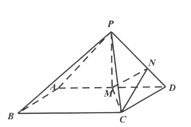
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com