已知函数f(x)=x3+ax2+bx+c在x=-2处取得极值,并且它的图象与直线y=-3x+3在点(1,0)处相切,
(1)求f(x)的解析式;
(2)求f(x)的单调区间.
解:(1)∵f′(x)=3x
2+2ax+b,
∴f′(-2)=3×(-2)
2+2a×(-2)+b=0
∴12-4a+b=0 ①又f′(1)=3+2a+b=-3 ②,由①②解得a=1,b=-8
又f(x)过点(1,0),
∴1
3+a×1
2+b×1+c=0,∴c=6
所以f(x)的解析式为:f(x)=x
3+x
2-8x+6
(2)由(1)知:f(x)=x
3+x
2-8x+6,所以f′(x)=3x
2+2x-8
令3x
2+2x-8<0解得
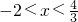
,令3x
2+2x-8>0解得x<-2,或

故f(x)的单调递增区间为(-∞,-2)和(

,+∞),
f(x)的单调递减区间为(-2,

)
分析:(1)求出f′(x),因为函数在x=-2处取得极值,所以f′(-2)=0,又因为函数与直线在点 (1,0 )处相切,所以f′(1)=-3,代入求得两个关于a与b的二元一次方程,求出解集得到a和b,又因为函数过点(1,0),代入求出c的值即可.
(2)由(1)求出的值可得导函数的解析式,分别令其大于、小于0可求增、减区间.
点评:考本题查学生利用导数研究函数极值的能力,及会求二元一次方程组解集和一元二次不等式解集的能力,属中档题.

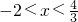 ,令3x2+2x-8>0解得x<-2,或
,令3x2+2x-8>0解得x<-2,或
 ,+∞),
,+∞), )
)

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<