
分析 (1)求出函数的导数,根据f′(1)=0,求出a的值检验即可;
(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出f(x)的范围,解关于b的不等式,求出b的范围即可.
解答 解:(1)f′(x)=3x2lnx+x2+3ax2,
由题意得:f′(1)=0,a=-$\frac{1}{3}$,
经检验符合题意,
故a=-$\frac{1}{3}$;
(2)f(x)=x3lnx-$\frac{1}{3}$x3+b,(x>0),
∴f′(x)=3x2lnx,
令f′(x)>0,解得:x>1,
令f′(x)<0,解得:x<1,
∴f(x)在($\frac{1}{e}$,1)递减,在(1,e)递增,
又f(1)=-$\frac{1}{3}$+b,f(e)=$\frac{{2e}^{3}}{3}$+b,
f($\frac{1}{e}$)=-$\frac{4}{{3e}^{3}}$+b,f(e)>f($\frac{1}{e}$),
∴x∈[$\frac{1}{e}$,e]时,f(x)∈[-$\frac{1}{3}$+b,$\frac{{2e}^{3}}{3}$+b],
由题意得:-$\frac{1}{3}$+b>0或$\frac{{2e}^{3}}{3}$+b<0,
故b>$\frac{1}{3}$或b<-$\frac{{2e}^{3}}{3}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要非充分条件 | B. | 充分非必要条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
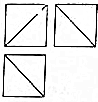 一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,已知三视图中每个正方形边长为1,则此三视图所对应几何体的体积为( )
一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,已知三视图中每个正方形边长为1,则此三视图所对应几何体的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
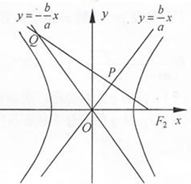 过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的右焦点F2向其一条渐近线作垂线l,垂足为P,l与另一条渐近线交于Q点,若$\overrightarrow{Q{F}_{2}}$=3$\overrightarrow{P{F}_{2}}$,则双曲线的离心率为( )
过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的右焦点F2向其一条渐近线作垂线l,垂足为P,l与另一条渐近线交于Q点,若$\overrightarrow{Q{F}_{2}}$=3$\overrightarrow{P{F}_{2}}$,则双曲线的离心率为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com